Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-16T19:17:56.633Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SINGULAR STATIONARITY II (TIGHT STATIONARITY AND EXTENDERS-BASED METHODS)

Published online by Cambridge University Press:  14 March 2019

OMER BEN-NERIA
OMER BEN-NERIA*
Affiliation:
INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEM JERUSALEM 91904, ISRAELE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the notion of tightly stationary sets which was introduced by Foreman and Magidor in [8]. We obtain two consistency results showing that certain sequences of regular cardinals 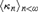${\langle {\kappa _n}\rangle _{n < \omega }}$ can have the property that in some generic extension, every ground-model sequence of fixed-cofinality stationary sets 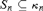${S_n} \subseteq {\kappa _n}$ is tightly stationary. The results are obtained using variations of the short-extenders forcing method.

Keywords

03E0403E3503E55singular cardinaltight stationarityPrikry forcingextender forcing
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 1 , March 2019 , pp. 320 - 342
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baumgartner, J. E., On the size of closed unbounded sets. Annals of Pure and Applied Logic, vol. 54 (1991), no. 3, pp. 195–227.10.1016/0168-0072(91)90047-PCrossRefGoogle Scholar
Ben-Neria, O., On singular stationarity I (mutual stationarity and ideal-based methods), preprint.Google Scholar
Chen, W., Tight stationarity and tree-like scales. Annals of Pure and Applied Logic, vol. 166 (2015), pp. 1019–1036.10.1016/j.apal.2015.05.004CrossRefGoogle Scholar
Chen, W. and Neeman, I., On the relationship between mutual and tight stationarity, preprint.Google Scholar
Cummings, J., Foreman, M., and Magidor, M., Canonical structure in the universe of set theory: Part one. Annals of Pure and Applied Logic, vol. 129 (2004), no. 1, pp. 211–243.10.1016/j.apal.2004.04.002CrossRefGoogle Scholar
Cummings, J., Foreman, M., and Magidor, M., Canonical structure in the universe of set theory: Part two. Annals of Pure and Applied Logic, vol. 142 (2006), no. 1, pp. 55–75.10.1016/j.apal.2005.11.007CrossRefGoogle Scholar
Foreman, M. and Magidor, M., A very weak square principle, this Journal, vol. 62 (1997), no. 1, pp. 175–196.Google Scholar
Foreman, M. and Magidor, M., Mutually stationary sequences of sets and the non-saturation of the non-stationary ideal on ${{\cal P}_\chi }\left( \lambda \right)$. Acta Mathematica, vol. 186 (2001), no. 2, pp. 271–300.10.1007/BF02401842CrossRefGoogle Scholar
Gitik, M., Prikry-type forcings,Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer Netherlands, Dordrecht, 2010, pp. 1351–1447.10.1007/978-1-4020-5764-9_17CrossRefGoogle Scholar
Gitik, M., Short extenders forcings I. Journal of Mathematical Logic, vol. 12 (2012), no. 02, p. 1250009.10.1142/S0219061312500092CrossRefGoogle Scholar
Gitik, M. and Unger, S., Short extender forcing, Appalachian Set Theory; 2006–2012 (Cummings, J. and Schimmerling, E., editors), London Mathematical Society Lecture Note Series 406, Cambridge University Press, Cambridge, 2012, pp. 245–264.10.1017/CBO9781139208574.009CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite, Springer-Verlag, Berlin, Heidelberg, 2003.Google Scholar
Shelah, S., Cardinal Arithmetic, Oxford University Press, Oxford, United Kingdom, 1994.Google Scholar
Sinapova, D. and Unger, S., Combinatorics at ${\aleph _\omega }$. Annals of Pure and Applied Logic, vol. 165 (2014), no. 4, pp. 996–1007.10.1016/j.apal.2013.12.001CrossRefGoogle Scholar
Unger, S., Gitik’s gap 2 short extender forcing with collapses, research note.Google Scholar