Published online by Cambridge University Press: 12 August 2016
We say a structure 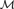 ${\cal M}$ in a first-order language
${\cal M}$ in a first-order language  ${\cal L}$ is indivisible if for every coloring of its universe in two colors, there is a monochromatic substructure
${\cal L}$ is indivisible if for every coloring of its universe in two colors, there is a monochromatic substructure 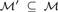 ${\cal M}\prime \subseteq {\cal M}$ such that
${\cal M}\prime \subseteq {\cal M}$ such that 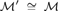 ${\cal M}\prime \cong {\cal M}$. Additionally, we say that
${\cal M}\prime \cong {\cal M}$. Additionally, we say that 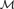 ${\cal M}$ is symmetrically indivisible if
${\cal M}$ is symmetrically indivisible if 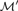 ${\cal M}\prime$ can be chosen to be symmetrically embedded in
${\cal M}\prime$ can be chosen to be symmetrically embedded in 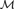 ${\cal M}$ (that is, every automorphism of
${\cal M}$ (that is, every automorphism of 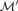 ${\cal M}\prime$ can be extended to an automorphism of
${\cal M}\prime$ can be extended to an automorphism of 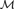 ${\cal M}$). Similarly, we say that
${\cal M}$). Similarly, we say that 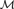 ${\cal M}$ is elementarily indivisible if
${\cal M}$ is elementarily indivisible if 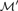 ${\cal M}\prime$ can be chosen to be an elementary substructure. We define new products of structures in a relational language. We use these products to give recipes for construction of elementarily indivisible structures which are not transitive and elementarily indivisible structures which are not symmetrically indivisible, answering two questions presented by A. Hasson, M. Kojman, and A. Onshuus.
${\cal M}\prime$ can be chosen to be an elementary substructure. We define new products of structures in a relational language. We use these products to give recipes for construction of elementarily indivisible structures which are not transitive and elementarily indivisible structures which are not symmetrically indivisible, answering two questions presented by A. Hasson, M. Kojman, and A. Onshuus.