No CrossRef data available.
Article contents
ON 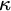 $\kappa $-HOMOGENEOUS, BUT NOT
$\kappa $-HOMOGENEOUS, BUT NOT 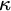 $\kappa $-TRANSITIVE PERMUTATION GROUPS
$\kappa $-TRANSITIVE PERMUTATION GROUPS
Published online by Cambridge University Press: 13 August 2021
Abstract
A permutation group G on a set A is
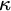 ${\kappa }$
-homogeneous iff for all
${\kappa }$
-homogeneous iff for all
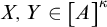 $X,Y\in \bigl [ {A} \bigr ]^ {\kappa } $
with
$X,Y\in \bigl [ {A} \bigr ]^ {\kappa } $
with
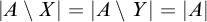 $|A\setminus X|=|A\setminus Y|=|A|$
there is a
$|A\setminus X|=|A\setminus Y|=|A|$
there is a
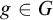 $g\in G$
with
$g\in G$
with
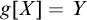 $g[X]=Y$
. G is
$g[X]=Y$
. G is
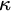 ${\kappa }$
-transitive iff for any injective function f with
${\kappa }$
-transitive iff for any injective function f with
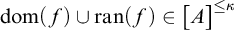 $\operatorname {dom}(f)\cup \operatorname {ran}(f)\in \bigl [ {A} \bigr ]^ {\le {\kappa }} $
and
$\operatorname {dom}(f)\cup \operatorname {ran}(f)\in \bigl [ {A} \bigr ]^ {\le {\kappa }} $
and
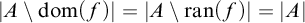 $|A\setminus \operatorname {dom}(f)|=|A\setminus \operatorname {ran}(f)|=|A|$
there is a
$|A\setminus \operatorname {dom}(f)|=|A\setminus \operatorname {ran}(f)|=|A|$
there is a
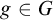 $g\in G$
with
$g\in G$
with
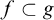 $f\subset g$
.
$f\subset g$
.
Giving a partial answer to a question of P. M. Neumann [6] we show that there is an
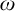 ${\omega }$
-homogeneous but not
${\omega }$
-homogeneous but not
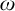 ${\omega }$
-transitive permutation group on a cardinal
${\omega }$
-transitive permutation group on a cardinal
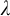 ${\lambda }$
provided
${\lambda }$
provided
-
(i)
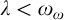 ${\lambda }<{\omega }_{\omega }$
, or
${\lambda }<{\omega }_{\omega }$
, or -
(ii)
 $2^{\omega }<{\lambda }$
, and
$2^{\omega }<{\lambda }$
, and
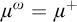 ${\mu }^{\omega }={\mu }^+$
and
${\mu }^{\omega }={\mu }^+$
and
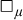 $\Box _{\mu }$
hold for each
$\Box _{\mu }$
hold for each
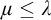 ${\mu }\le {\lambda }$
with
${\mu }\le {\lambda }$
with
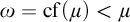 ${\omega }=\operatorname {cf}({\mu })<{{\mu }}$
, or
${\omega }=\operatorname {cf}({\mu })<{{\mu }}$
, or -
(iii) our model was obtained by adding
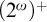 $(2^{\omega })^+$
many Cohen generic reals to some ground model.
$(2^{\omega })^+$
many Cohen generic reals to some ground model.
For
 ${\kappa }>{\omega }$
we give a method to construct large
${\kappa }>{\omega }$
we give a method to construct large
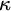 ${\kappa }$
-homogeneous, but not
${\kappa }$
-homogeneous, but not
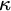 ${\kappa }$
-transitive permutation groups. Using this method we show that there exist
${\kappa }$
-transitive permutation groups. Using this method we show that there exist
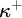 ${\kappa }^+$
-homogeneous, but not
${\kappa }^+$
-homogeneous, but not
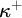 ${\kappa }^+$
-transitive permutation groups on
${\kappa }^+$
-transitive permutation groups on
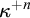 ${\kappa }^{+n}$
for each infinite cardinal
${\kappa }^{+n}$
for each infinite cardinal
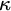 ${\kappa }$
and natural number
${\kappa }$
and natural number
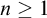 $n\ge 1$
provided
$n\ge 1$
provided
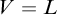 $V=L$
.
$V=L$
.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



