Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T17:58:49.787Z Has data issue: false hasContentIssue false
  • English
  • Français

On ideals of subsets of the plane and on Cohen reals

Published online by Cambridge University Press:  12 March 2014

Jacek Cichoń  and
Janusz Pawlikowski
Jacek Cichoń
Affiliation:
Instytut Matematyczny, Universytet Wrocław, 50-384 Wrocław, Poland
Janusz Pawlikowski
Affiliation:
Instytut Matematyczny, Universytet Wrocław, 50-384 Wrocław, Poland
Get access Rights & Permissions [Opens in a new window]

Abstract

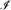Let be any proper ideal of subsets of the real line R which contains all finite subsets of R. We define an ideal 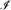* ∣ 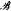as follows: X ∈ 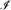* ∣ 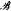if there exists a Borel set B ⊂ R × R such that X ⊂ B and for any x ∈ R we have {y ∈ R: 〈x, y〉 ∈ B} ∈ 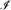. We show that there exists a family 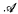⊂ 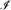* ∣ 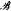of power ω1 such that ⋃ ∉ * ∣ .

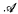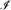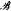In the last section we investigate properties of ideals of Lebesgue measure zero sets and meager sets in Cohen extensions of models of set theory.

Keywords

Lebesgue measureBaire categorycardinal indicesCohen reals.
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 3 , September 1986 , pp. 560 - 569
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartoszyński, T., Additivity of measure implies additivity of category, Transactions of the American Mathematical Society, vol. 281 (1984), pp. 209–213.CrossRefGoogle Scholar
[2]Cenzer, D. and Maudlin, R.D., Inductive definability: measure and category, Advances in Mathematics, vol. 38 (1980), pp. 55–90.CrossRefGoogle Scholar
[3]Cichoń, J., On bases of ideals and Boolean algebras, Open days for model theory and set theory, Jadwisin 1981 (Guzicki, W.et al, editors) (to appear).Google Scholar
[4]Cichoń, J., On random reals and the measure algebra (to appear).Google Scholar
[5]Fremlin, D., On Cichoń's diagrams, preprint, 1984.Google Scholar
[6]Fremlin, D., Consequences of Martin's axiom, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
[7]Koepke, P., Can adding a Cohen real destroy the existence of a scale?Open days for model theory and set theory, Jadwisin 1981 (Guzicki, W.et al, editors) (to appear).Google Scholar
[8]Krawczyk, A., A note on random reals, preprint, 1983.Google Scholar
[9]Kuratowski, K., Topologie, Vol. 1, PWN, Warsaw, 1958.Google Scholar
[10]Kuratowski, K. and Mostowski, A., Set theory, PWN, Warsaw, and North-Holland, Amsterdam, 1976.Google Scholar
[11]Martin, D. A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[12]Miller, A., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114.CrossRefGoogle Scholar
[13]Miller, A., Additivity of measure implies dominating reals, Proceedings of the American Mathematical Society, vol. 91 (1984), pp. 111–117.CrossRefGoogle Scholar
[14]Moschovakis, Y. N., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[15]Pawlikowski, J., Why Solovay real produces Cohen real, this Journal (to appear).Google Scholar
[16]Rothberger, F., Eine Äquivalenz zwischen der Kontinuumhypothese und der Existenz der Luzinschen und Sierpińflskischen Mengen, Fundamenta Mathematic, vol. 30 (1938), pp. 215–217.CrossRefGoogle Scholar
[17]Sikorski, R., Boolean algebras, Springer-Verlag, Berlin, 1964.Google Scholar
[18]Solovay, R., A model of set theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar
[19]Truss, J. K., Sets having calibre ℵ1, Logic Colloquium 76, North-Holland, Amsterdam, 1977, pp. 595–612.Google Scholar
[20]Truss, J. K., The noncommutativity of random and generic extensions, this Journal, vol. 48 (1983), pp. 1009–1012.Google Scholar