Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-09T07:16:56.015Z Has data issue: false hasContentIssue false
  • English
  • Français

On existence conditions for elements and classes

Published online by Cambridge University Press:  12 March 2014

W. V. Quine
W. V. Quine*
Affiliation:
Harvard University
Get access Rights & Permissions [Opens in a new window]

Extract

In the middle of my Mathematical logic I defined a certain class of formulae as “stratified,” and conjectured that exclusion from this class is a feature “shared, presumably, by all the untenable statements 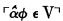(p. 157). This ushered in a set of axioms of class-membership which Rosser has since shown to be inconsistent. Accordingly, in Element and number I dropped the principle *200, in which had been assembled axioms to the effect, roughly, that “stratified functions of elements are elements.” In lieu of *200 I set forth alternatives in which no appeal is made to stratification. The system of Mathematical logic exclusive of *200 carries over as an unchanging framework; and this framework admits, we know, of a simple consistency proof. My concern in the present paper is to draw attention to certain relationships between this framework and earlier theories.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 7 , Issue 4 , December 1942 , pp. 157 - 159
Copyright
Copyright © Association for Symbolic Logic 1943

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Rosser, Barkley, The Burali-Forti paradox, this Journal, vol. 7 (1942), pp. 1–17.Google Scholar

2 This Journal, vol. 6 (1941), pp. 135–149.

8 The utility of the stratification concept is not, indeed, quite discredited. The system of my New foundations for mathematical logic (The American mathematical monthly, vol. 44 (1937), pp. 70–80), which uses stratification as a condition of class existence rather than of elementhood, is not yet known to be inconsistent.

4 Cf. Element and number, p. 135.

5 Cf. Mathematical logic p. 161; also D10.

6 Bernays, Paul, A system of axiomatic set theory—Part I, this Journal, vol. 2 (1937), pp. 65–77.Google Scholar

7 Bernays, op. cit., p. 65. Neumann, J. von, Eine Axiomatisierung der Mengenlehre, Journal für die reine und angewandte Mathematik, vol. 154 (1925), pp. 219–240.Google Scholar

8 Not because of complications that would arise from the further quantifications which appear within when abbreviations are expanded.

9 Cf. Bernays, op. cit., p. 72. He formulates his principle in extension to “κ-tuplets,” but this extension is derivable from the above version.

10 Zermelo, Ernst, Untersuchungen über die Grundlagen der Mengenlehre I, Mathematische Annalen, vol. 65 (1908), pp. 261–281.CrossRefGoogle Scholar

11 Skolem, Thoralf, Einige Bemerkungen zu der Abhandlung von E. Zermelo, Fundamenta mathematicae, vol. 15 (1930), pp. 337–341.CrossRefGoogle Scholar