Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T14:05:32.923Z Has data issue: false hasContentIssue false
  • English
  • Français

On Diophantine equations solvable in models of open induction

Published online by Cambridge University Press:  12 March 2014

Margarita Otero
Margarita Otero*
Affiliation:
Mathematical Institute, Oxford OX1 3LB, England
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider IOpen, the subsystem of PA (Peano Arithmetic) with the induction scheme restricted to quantifier-free formulas.

We prove that each model of IOpen can be embedded in a model where the equation 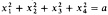has a solution. The main lemma states that there is no polynomial f{x,y) with coefficients in a (nonstandard) DOR M such that ∣f(x,y) ∣ < 1 for every (x,y) Є C, where C is the curve defined on the real closure of M by C: x2 + y2 = a and a > 0 is a nonstandard element of M.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 2 , June 1990 , pp. 779 - 786
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Borevich, Z. I. and Shavarevich, I. R., Number theory, Academic Press, New York, 1968.Google Scholar
[2]van den Dries, L., Some model theory and number theory for models of weak systems of arithmetic, Model theory of algebra and arithmetic (Karpacz, 1979; Pacholski, L.et al., editors), Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 346–362.CrossRefGoogle Scholar
[3]Macintyre, A. J. and Marker, D., Primes and their residue rings in models of open induction, Annals of Pure and Applied Logic, vol. 43 (1989), pp. 57–77.CrossRefGoogle Scholar
[4]Shepherdson, J. C., A non-standard model for a free variable fragment of number theory, Bulletin de l'Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 12 (1964), pp. 79–86.Google Scholar
[5]Wilkie, A. J., Some results and problems on weak systems of arithmetic, Logic Colloquium '77 (Macintyre, A. J.et al., editors), North-Holland, Amsterdam, 1978, pp. 285–296.CrossRefGoogle Scholar

A correction has been issued for this article:

Corrigendum

Margarita Otero