Published online by Cambridge University Press: 12 March 2014
1. The notion of derivability. Italic capitals, with or without subscripts, will be used as variables. They are to take as values some manner of elements which may for the present be left undetermined. Now let us consider abstractly the notion of the derivability of an element X from one or more specified elements by a series of steps of a specified kind. This involves reference to two conditions upon elements. One of these conditions, expressible by some statement form containing a single free variable, determines the elements from which X is said to be derivable. The other condition, expressed say by a statement form containing k + 1 free variables, determines the kind of steps by which the derivation is to proceed; it is the condition which any elements Z1, … Zk, Y must fulfill if progress from Zi, …, Zk to Y is to constitute a step of derivation in the intended sense. Supposing “f(Y)” supplanted by the first of these statement forms, whatever it may be, and “g(Z1, …, Zk, Y)” supplanted by the other, let us adopt the form of notation
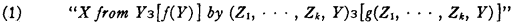
to express derivability of X in the suggested sense. The meaning of (1) can be formulated more accurately as follows:
(i) There are elements Y1 to Ym (for some m) such that Ym = X and, for each i≦m, either f(Yi) or else there are numbers j1 to Ym, each less than i, for which g(Yj1, …, Yjk, Yi).
(Variable subscripts are to be understood, here and throughout the paper, as referring only to positive integers.)
The notion (1) is illustrated in the ancestral R* of a relation R;1 for,
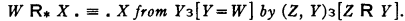
Another illustration is afforded by metamathematics. Suppose our elements are the expressions used in some formal system; suppose we have defined “Post(Y)”, meaning that Y is a postulate of that system; and suppose we have defined “Inf(ZI, …, Zk, Y)” (for some fixed k large enough for all purposes of the system in question), meaning that Y proceeds from Z1, …, Zk by one application of one or another of the rules of inference of the system. Then
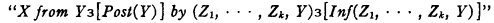
would mean that X is a theorem of the system.
1 See Whitehead, and Russell, , Principia mathematica, vol. 1, pp. 543–544Google Scholar.
2 Cf. Kleene, , General recursive functions of natural numbers, Mathemalische Annale, vol. 112 (1936), p. 727CrossRefGoogle Scholar.
3 Contextual definition of this device does not require use of propositional-function variables as in Principia mathematica. We have only to exhaust the minimum contexts of variables for the primitive language at hand, as illustrated in my New foundations for mathematical logic, The American mathematical monthly, vol. 44 (1937), pp. 74–75Google Scholar.
4 See Gödel, , Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, Monatshefte für Mathematik und Physik, vol. 38 (1931), pp. 173–198CrossRefGoogle Scholar. Let us understand the word “incompletability” as carrying with it the various qualifications which enter the full statement of Gödel's result.
5 I have carried this through in detail for a particular formal system involving just the concepts specified above for Σ. Publication of the details would not justify the excessive space required, for the essential steps are apparent from Gödel's paper and the present one.
6 See pp. 72–73 of my previously cited paper.
7 These are taken from my Definition of substitution, Bulletin of the American Mathematical Society, vol. 42 (1936), p. 562Google Scholar.