Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T00:41:18.375Z Has data issue: false hasContentIssue false
  • English
  • Français

On carnap and popper probability functions

Published online by Cambridge University Press:  12 March 2014

Hugues Leblanc  and
Bas C. van Fraassen
Hugues Leblanc
Affiliation:
Temple University, Philadelphia, PA 19122 University of Toronto, Toronto, CanadaM5S 1A1 University of Southern California, Los Angeles, CA 90007
Bas C. van Fraassen
Affiliation:
Temple University, Philadelphia, PA 19122 University of Toronto, Toronto, CanadaM5S 1A1 University of Southern California, Los Angeles, CA 90007
Get access Rights & Permissions [Opens in a new window]

Extract

With PC understood to be the propositional calculus of [3], call a binary function Pr from the wffs of PC to the reals a Carnap (probability) function if it meets requirements A1—A5 in Table I (with ‘⊢…’ short in A3—A4 for ‘… is a tautology’), and call the function a Popper (probability) function if it meets requirements Bl—B6 there:

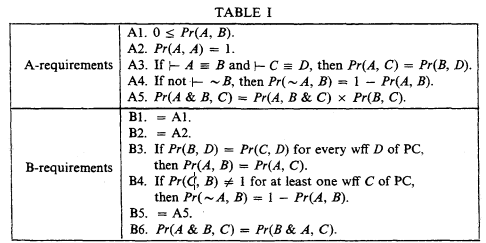
Leblanc established in [3] that every Carnap function is a Popper one, and he tendered proof of the converse. As reported by Stalnaker in [5], the proof unfortunately was incomplete, a mishap due to Leblanc's abbreviating ‘Pr(A, ∼ A) = 1’ as ‘⊢ A’ when Pr is a Popper function. Borrowing from [4], Leblanc did show, as Harper notes in [2, footnote 17], that

(1) If Pr is a Popper function and A is a tautology, then Pr(A, ∼ A) = 1. He did not, however, show that

(2) If Pr is a Popper function and Pr(A, ∼ A) = 1, then A is a tautology.

Nor could he have done so: (2) is false, as the simplest of counterexamples shows. Denied (2), Leblanc had no hope of proving that every Popper function is a Carnap one: of a Popper function Pr it is easily ascertained that Pr meets requirement A4 if and only if Pr(A, ∼ A) = 1 just in case A is a tautology.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 369 - 373
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carnap, R., Logical foundations of probability, University of Chicago Press, Chicago, 1950.Google Scholar
[2]Harper, W. L., Rational belief change, Popper functions and counterfactuals, Foundations of probability theory, statistical inference, and statistical theories of science, vol. I, Reidel, Dordrecht, pp. 73–115, 1976.CrossRefGoogle Scholar
[3]Leblanc, H., On requirements for conditional probability functions, this Journal, vol. 25 (1960), pp. 238–242.Google Scholar
[4]Popper, K. R., The logic of scientific discovery, Basic Books, Inc., New York, 1959.Google Scholar
[5]Stalnaker, R. C., Probability and conditionals, Philosophy of Science, vol. 37 (1970), pp. 64–80.CrossRefGoogle Scholar
[6]van Fraassen, B. C., Representation of conditional probabilities, Journal of Philosophical Logic, vol. 5 (1976), pp. 417–430 (corrigendum 6: p. 365).CrossRefGoogle Scholar