Article contents
On Cantor-Bendixson spectra containing (1,1). II1
Published online by Cambridge University Press: 12 March 2014
Extract
Let T be a (countable, complete, quantifier eliminable) ω-stable theory; an analysis of T, and consequently a classification of ω-stable theories, can be done by looking at the Boolean algebras B(M) of definable subsets of its countable models M (as usual, we often confuse a definable subset of M with the class of formulas defining it). If M ⊨ T, ∣M∣ = ℵ0, then, for every LM-formula ϕ(v) and for every ordinal α, we define a relation
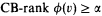
(CB = Cantor-Bendixson, of course) by induction on α:
CB-rank ϕ(v) ≥ 0 if ϕ(M) ≠ ∅
CB-rank ϕ(v) ≥ λ for λ a limit ordinal, if CB-rank ϕ(v) ≥ for all v < λ;
CB-rank ϕ(v)≥ α + 1 if, for all n ∈ ω,
(*) there are LM-formulas ϕ0(v), …, ϕn − 1(v) such that
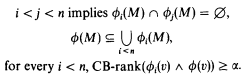
It is well known that the ω-stability of T implies that, for every consistent LM-formula ϕ(v), there is exactly one ordinal α < ω1 such that CB-rank ϕ(v) ≥ α and CB-rank ϕ(v)≱α + 1. Therefore we define:
CB-rank ϕ(v) = α
CB-degree ϕ(v) = d if d is the maximal n ∈ ω satisfying (*); and
CB-type ϕ(v) = (α, d).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
Footnotes
Work performed under the auspices of Italian C.N.R. (G.N.S.A.G.A.).
References
REFERENCES
- 1
- Cited by


