In this paper, we study finitely axiomatizable conservative extensions of a theory U in the case where U is recursively enumerable and not finitely axiomatizable. Stanisław Krajewski posed the question whether there are minimal conservative extensions of this sort. We answer this question negatively.

Consider a finite expansion of the signature of U that contains at least one predicate symbol of arity ≥ 2. We show that, for any finite extension α of U in the expanded language that is conservative over U, there is a conservative extension β of U in the expanded language, such that 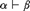$\alpha \vdash \beta$ and 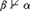$\beta \not \vdash \alpha$. The result is preserved when we consider either extensions or model-conservative extensions of U instead of conservative extensions. Moreover, the result is preserved when we replace $\dashv$ as ordering on the finitely axiomatized extensions in the expanded language by a relevant kind of interpretability, to wit interpretability that identically translates the symbols of the U-language.

We show that the result fails when we consider an expansion with only unary predicate symbols for conservative extensions of U ordered by interpretability that preserves the symbols of U.