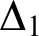Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-06T11:50:35.415Z Has data issue: false hasContentIssue false
  • English
  • Français

NS SATURATED AND ${\Delta }_{1}$-DEFINABLE

Part of: Set theory

Published online by Cambridge University Press:  16 February 2021

STEFAN HOFFELNER
STEFAN HOFFELNER*
Affiliation:
WESTFÄLISCHE WILHELMS UNIVERSITÄT, MÜNSTER MÜNSTER, GERMANYE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

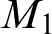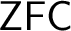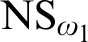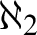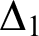We show that under the assumption of the existence of the canonical inner model with one Woodin cardinal $M_1$ , there is a model of $\mathsf {ZFC}$ in which $\mbox {NS}_{\omega _{1}}$ is $\aleph _2$ -saturated and ${\Delta }_{1}$ -definable with 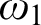$\omega _1$ as a parameter which answers a question of S. D. Friedman and L. Wu. 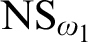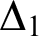We also show that starting from an arbitrary universe with a Woodin cardinal, there is a model with $\mbox {NS}_{\omega _{1}}$ saturated and ${\Delta }_{1}$ -definable with a ladder system 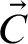$\vec {C}$ and a full Suslin tree T as parameters. Both results rely on a new coding technique whose presentation is the main goal of this article .

Keywords

nonstationary idealdefinabilitycodinginner modelslarge cardinals

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E45: Inner models, including constructibility, ordinal definability, and core models 03E55: Large cardinals 03E57: Generic absoluteness and forcing axioms
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 1 , March 2021 , pp. 25 - 59
Check for updates
Copyright
© The Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baumgartner, J., Applications of the proper forcing axiom , Handbook of Set-Theoretic Topology (Kunen, K. and Jerry, V., editors), North-Holland, Amsterdam, 1984, pp. 913–959.CrossRefGoogle Scholar
Caicedo, A. and Friedman, S. D., BPFA and projective wellorderings of the reals , this Journal vol. 76 (2011), pp. 1126–1136.Google Scholar
Caicedo, A. and Velickovic, B., The bounded proper forcing axiom and wellorderings of the reals . Mathematical Research Letters , vol. 13 (2006), nos. 2–3, pp. 393–408.CrossRefGoogle Scholar
Fischer, V. and Friedman, S. D., Cardinal characteristics and projective wellorders . Annals of Pure and Applied Logic , vol. 161 (2010), pp. 916–922.CrossRefGoogle Scholar
Friedman, S. D., Hyttinen, T., and Kulikov, V., Generalized Descriptive Set Theory , Memoirs of the American Mathematical Society, AMS, Providence, RI, 2014.Google Scholar
Friedman, S. D. and Wu, L., Large cardinals and the ${\varDelta}_1$ -definability of the nonstationary ideal . Preprint.Google Scholar
Friedman, S. D., Wu, L., and Zdomskyy, L., ${\varDelta}_1$ -Definability of the nonstationary ideal at successor cardinals . Fundamenta Mathematicae , vol. 229 (2015), pp. 231–254.CrossRefGoogle Scholar
Hoffelner, S., Projective well-orders and the nonstationary ideal, Ph.D. thesis, University of Vienna, 2016.Google Scholar
Harrington, L., Long projective wellorderings . Annals of Mathematical Logic , vol. 12 (1977), no.1, pp. 1–24.CrossRefGoogle Scholar
Hyttinen, T. and Rautila, M., The canary tree revisited , this Journal, vol. 66 (2001), no. 4, pp. 1677–1694.Google Scholar
Jech, T., Set Theory. Springer, Berlin, Germany, 2003.Google Scholar
Jensen, R. B. and Solovay, R. M., Some applications of almost disjoint sets , Mathematical Logic and Foundations of Set Theory (Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
Larson, P., Saturation, Suslin trees and meager sets . Archive for Mathematical Logic , vol. 44 (2005), pp. 581–595.CrossRefGoogle Scholar
Lücke, P., Schindler, R., and Schlicht, P., ${\varSigma}_1(\kappa)$ -definable subsets of $\left({\kappa}^{+}\right)$ , this Journal, vol. 82 (2017), no. 3, pp. 1106–1131.Google Scholar
Mekler, A. H. and Shelah, S., The canary tree . Canadian Mathematical Bulletin , vol. 36 (1993), no. 2, pp. 209–215.CrossRefGoogle Scholar
Miyamoto, T., On iterating semiproper preorders , this Journal, vol. 67 (2002), pp. 1431–1468.Google Scholar
Miyamoto, T., ${\omega}_1$ -Suslin trees under countable support iterations . Fundamenta Mathematicae , vol. 143 (1993), pp. 257–261.CrossRefGoogle Scholar
Moore, J., Set mapping reflection . Journal of Mathematical Logic , vol. 05 (2005), no. 01, pp. 87–97.CrossRefGoogle Scholar
Schindler, R., On $\mathrm{NS}{\omega}_1$ being saturated. Online notes. Available at http://www.math.uni-muenster.de/u/rds/sat_ideal_better_version.pdf (accessed 20 June, 2016).Google Scholar
Shelah, S., Projectively well-ordered inner models . Annals of Pure and Applied Logic , vol. 74 (1995), pp.77–104.Google Scholar
Shelah, S., An outline of inner model theory, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Berlin, Germany, 2010, pp. 1595–1684.Google Scholar
Shelah, S., Proper and Improper Forcing , Springer, Berlin, Germany, 2017.Google Scholar
Woodin, H. W., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal , De Gruyter, Berlin, Germany, 2001.Google Scholar