Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T04:39:29.180Z Has data issue: false hasContentIssue false
  • English
  • Français

A normalization theorem for set theory1

Published online by Cambridge University Press:  12 March 2014

Sidney C. Bailin
Sidney C. Bailin*
Affiliation:
Computer Technology Associates, 14900 Sweitzer Lane, Suite 201, Laurel, Maryland 20707
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we present a normalization theorem for a natural deduction formulation of Zermelo set theory. Our result gets around M. Crabbe's counterexample to normalizability (Hallnäs [3]) by adding an inference rule of the form

and requiring that this rule be used wherever it is applicable. Alternatively, we can regard the result as pertaining to a modified notion of normalization, in which an inference

is never considered reducible if A is T Є T, even if R is an elimination rule and the major premise of R is the conclusion of an introduction rule. A third alternative is to regard (1) as a derived rule: using the general well-foundedness rule

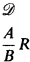
we can derive (1). If we regard (2) as neutral with respect to the normality of derivations (i.e., (2) counts as neither an introduction nor an elimination rule), then the resulting proofs are normal.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 3 , September 1988 , pp. 673 - 695
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This material is based upon work supported by the National Science Foundation under award number ISI-8560438. Any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author and do not necessarily reflect the views of the National Science Foundation.

References

REFERENCES

[1]Barendregt, H. P., The lambda calculus—its syntax and semantics, North-Holland, Amsterdam, 1981.Google Scholar
[2]Girard, J.-Y., Une extension de l'interpretation de Gödel à l'analyse, et son application à l'élimination des coupures dans l'analyse et la théorie des types, Proceedings of the second Scandinavian logic symposium (Fenstad, J., editor), North-Holland, Amsterdam, 1971, pp. 63–92.CrossRefGoogle Scholar
[3]Hallnäs, L., On normalization of proofs in set theory, Ph.D. thesis, University of Stockholm, Stockholm, 1983.Google Scholar
[4]Prawitz, D., Natural deduction, a proof-theoretic study, Almqvist & Wiksell, Stockholm, 1965.Google Scholar
[5]Statman, R., Structural complexity of proofs, Ph.D. thesis, Stanford University, Stanford, California, 1974.Google Scholar