No CrossRef data available.
Article contents
The nonconstructive content of sentences of arithmetic
Published online by Cambridge University Press: 12 March 2014
Extract
This note is concerned with the old topic, initiated by Kleene, of the connections between recursive function theory and provability in intuitionistic arithmetic. More specifically, we are interested in the relationship between the hierarchy of degrees of unsolvability and the interdeducibility of cases of excluded middle. The work described below was motivated by a counterexample, to be given presently, which shows that that relationship is more complicated than one might suppose.
Let HA be first-order intuitionistic arithmetic. Let the symbol ⊢ mean derivability in HA. For each natural number n, let n¯ be the corresponding numeral. Let Ω be the standard model of arithmetic. Say that a sentence ϕ is true iff Ω⊨ ϕ. Now suppose ϕ(x) and Ψ(x) are formulas with only the variable x free. Suppose
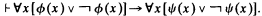
Then it is natural to conjecture that {n∣Ω⊨Ψ(n¯)} is recursive in {n∣Ω⊨ϕ(n¯)}.
However, this conjecture is false. Consider the formula is a formalization of Kleene's T-predicate.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978


