Published online by Cambridge University Press: 21 March 2017
The derivation on the differential-valued field Tlog of logarithmic transseries induces on its value group 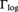 ${{\rm{\Gamma }}_{{\rm{log}}}}$ a certain map ψ. The structure
${{\rm{\Gamma }}_{{\rm{log}}}}$ a certain map ψ. The structure 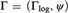 ${\rm{\Gamma }} = \left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ is a divisible asymptotic couple. In [7] we began a study of the first-order theory of
${\rm{\Gamma }} = \left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ is a divisible asymptotic couple. In [7] we began a study of the first-order theory of 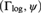 $\left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ where, among other things, we proved that the theory
$\left( {{{\rm{\Gamma }}_{{\rm{log}}}},\psi } \right)$ where, among other things, we proved that the theory 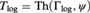 $T_{{\rm{log}}} = Th\left( {{\rm{\Gamma }}_{{\rm{log}}} ,\psi } \right)$ has a universal axiomatization, is model complete and admits elimination of quantifiers (QE) in a natural first-order language. In that paper we posed the question whether Tlog has NIP (i.e., the Non-Independence Property). In this paper, we answer that question in the affirmative: Tlog does have NIP. Our method of proof relies on a complete survey of the 1-types of Tlog, which, in the presence of QE, is equivalent to a characterization of all simple extensions
$T_{{\rm{log}}} = Th\left( {{\rm{\Gamma }}_{{\rm{log}}} ,\psi } \right)$ has a universal axiomatization, is model complete and admits elimination of quantifiers (QE) in a natural first-order language. In that paper we posed the question whether Tlog has NIP (i.e., the Non-Independence Property). In this paper, we answer that question in the affirmative: Tlog does have NIP. Our method of proof relies on a complete survey of the 1-types of Tlog, which, in the presence of QE, is equivalent to a characterization of all simple extensions 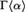 ${\rm{\Gamma }}\left\langle \alpha \right\rangle$ of
${\rm{\Gamma }}\left\langle \alpha \right\rangle$ of  ${\rm{\Gamma }}$. We also show that Tlog does not have the Steinitz exchange property and we weigh in on the relationship between models of Tlog and the so-called precontraction groups of [9].
${\rm{\Gamma }}$. We also show that Tlog does not have the Steinitz exchange property and we weigh in on the relationship between models of Tlog and the so-called precontraction groups of [9].