Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T04:51:21.147Z Has data issue: false hasContentIssue false
  • English
  • Français

The natural hierarchy and quasi-hierarchy of constructibility degrees

Published online by Cambridge University Press:  12 March 2014

Philip Welch
Philip Welch*
Affiliation:
Department of Mathematics, University of California at Los Angeles, Los Angeles, California 90024
Get access Rights & Permissions [Opens in a new window]

Abstract.

We investigate the set S2 of “quickly sharped” reals:

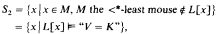
in the manner of [K] defining a natural hierarchy and quasi-hierarchy of constructibility degrees and identifying their termination points.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 1 , March 1986 , pp. 130 - 134
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[CM]Dodd, A. J., The core model, London Mathematical Society Lecture Note Series, vol. 61, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[CU]Beller, A., Jensen, R. B. and Welch, P. D., Coding the universe, London Mathematical Society Lecture Note Series, vol. 47, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[K]Kechris, A., The theory of countable analytic sets, Transactions of the American Mathematical Society, vol. 202 (1975), pp. 259–297.Google Scholar
[S]Sacks, G., Forcing with perfect closed sets, Axiomatic set theory (Scott, D. S., editor), Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, 1971, pp. 331–355.CrossRefGoogle Scholar
[W]Welch, P. D., Countable sequences of mice (typescript).Google Scholar
[W1]Welch, P. D., Minimal covers and constructibility degrees (typescript).Google Scholar