Article contents
MÜNCHHAUSEN PROVABILITY
Published online by Cambridge University Press: 10 June 2021
Abstract
By Solovay’s celebrated completeness result [31] on formal provability we know that the provability logic 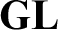 ${\textbf {GL}}$
describes exactly all provable structural properties for any sound and strong enough arithmetical theory with a decidable axiomatisation. Japaridze generalised this result in [22] by considering a polymodal version
${\textbf {GL}}$
describes exactly all provable structural properties for any sound and strong enough arithmetical theory with a decidable axiomatisation. Japaridze generalised this result in [22] by considering a polymodal version 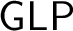 ${\mathsf {GLP}}$
of
${\mathsf {GLP}}$
of 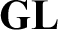 ${\textbf {GL}}$
with modalities
${\textbf {GL}}$
with modalities 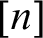 $[n]$
for each natural number n referring to ever increasing notions of provability. Modern treatments of
$[n]$
for each natural number n referring to ever increasing notions of provability. Modern treatments of 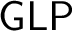 ${\mathsf {GLP}}$
tend to interpret the
${\mathsf {GLP}}$
tend to interpret the 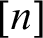 $[n]$
provability notion as “provable in a base theory T together with all true
$[n]$
provability notion as “provable in a base theory T together with all true 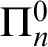 $\Pi ^0_n$
formulas as oracles.” In this paper we generalise this interpretation into the transfinite. In order to do so, a main difficulty to overcome is to generalise the syntactical characterisations of the oracle formulas of complexity
$\Pi ^0_n$
formulas as oracles.” In this paper we generalise this interpretation into the transfinite. In order to do so, a main difficulty to overcome is to generalise the syntactical characterisations of the oracle formulas of complexity 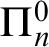 $\Pi ^0_n$
to the hyper-arithmetical hierarchy. The paper exploits the fact that provability is
$\Pi ^0_n$
to the hyper-arithmetical hierarchy. The paper exploits the fact that provability is 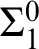 $\Sigma ^0_1$
complete and that similar results hold for stronger provability notions. As such, the oracle sentences to define provability at level
$\Sigma ^0_1$
complete and that similar results hold for stronger provability notions. As such, the oracle sentences to define provability at level 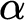 $\alpha $
will recursively be taken to be consistency statements at lower levels: provability through provability whence the name of the paper. The paper proves soundness and completeness for the proposed interpretation for a wide class of theories, namely for any theory that can formalise the recursion described above and that has some further very natural properties. Some remarks are provided on how the recursion can be formalised into second order arithmetic and on lowering the proof-theoretical strength of these systems of second order arithmetic.
$\alpha $
will recursively be taken to be consistency statements at lower levels: provability through provability whence the name of the paper. The paper proves soundness and completeness for the proposed interpretation for a wide class of theories, namely for any theory that can formalise the recursion described above and that has some further very natural properties. Some remarks are provided on how the recursion can be formalised into second order arithmetic and on lowering the proof-theoretical strength of these systems of second order arithmetic.
MSC classification
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2021
References
REFERENCES
- 2
- Cited by



