Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T06:02:52.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Models of transfinite provability logic

Published online by Cambridge University Press:  12 March 2014

David Fernández-Duque  and
Joost J. Joosten
David Fernández-Duque
Affiliation:
Department of Computer Science and Artificial Intelligence, Universidad de Sevilla, Av. Reina Mercedes S/N, 41012 Seville, Spain, E-mail:[email protected]
Joost J. Joosten
Affiliation:
Department of Logic, History and Philosophy of Science, University of Barcelona, C. Montalegre, 6, 08001 Barcelona, Spain, E-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

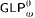For any ordinal Λ, we can define a polymodal logic GLPΛ, with a modality [ξ] for each ξ < Λ. These represent provability predicates of increasing strength. Although GLPΛ has no Kripke models, Ignatiev showed that indeed one can construct a Kripke model of the variable-free fragment with natural number modalities, denoted . Later, Icard defined a topological model for 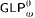which is very closely related to Ignatiev's.

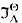In this paper we show how to extend these constructions for arbitrary Λ. More generally, for each Θ, Λ we build a Kripke model and a topological model 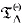, and show that 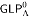is sound for both of these structures, as well as complete, provided Θ is large enough.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 2 , June 2013 , pp. 543 - 561
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Beklemishev, L. D., Fernández-Duque, D., and Joosten, J. J., On provability logics with linearly ordered modalities, forthcoming, 2012.Google Scholar
[2] Beklemishev, L. D. and Gabelaia, D., Topological completeness of the provability logicGLP, ArXiv, (2011), pp. 1–26.Google Scholar
[3] Beklemishev, L.D., Provability algebras and proof-theoretic ordinals, I, Annals of Pure and Applied Logic, vol. 128 (2004), pp. 103–124.CrossRefGoogle Scholar
[4] Beklemishev, L.D., Joosten, J.J., and Vervoort, M., A finitary treatment of the closed fragment of Japaridze's provability logic. Journal of Logic and Computation, vol. 15 (2005), pp. 447–463.CrossRefGoogle Scholar
[5] Fernández-Duque, D. and Joosten, J. J., Hyperations, Vehlen progressions and transfinite iteration of ordinal functions, submitted, 05 2012.Google Scholar
[6] Fernández-Duque, D., Kripke models of transfinite provability logic, Advances in modal logic, vol. 9, College Publications, 2012, pp. 185–199.Google Scholar
[7] Fernández-Duque, D., Turing progressions and their well-orders. How the world computes. Lecture Notes in Computer Science, Springer, 2012, pp. 212–221.CrossRefGoogle Scholar
[8] Fernández-Duque, D., Well-orders in the transfinite Japaridze algebra, submitted, 03 2012.Google Scholar
[9] Fernández-Duque, D., Well-orders in the transfinite Japaridze algebra II: Turing progressions and their well-orders, forthcoming, 2012.Google Scholar
[10] Icard, T. F. III, A topological study of the closed fragment of GLP, Journal of Logic and Computation, vol. 21 (2011), pp. 683–696.CrossRefGoogle Scholar
[11] Ignatiev, K.N., On strong provability predicates and the associated modal logics, this Journal, vol. 58 (1993), pp. 249–290.Google Scholar
[12] Japaridze, G., The polymodal provability logic, Intensional logics and logical structure of theories: material from the Fourth Soviet-Finnish symposium on logic, Metsniereba, Telavi, 1988, In Russian.Google Scholar
[13] Joosten, J. J., lntepretability formalized. Department of Philosophy, University of Utrecht, 2004, Ph.D. thesis.Google Scholar
[14] Segerberg, K., An essay in classical modal logic. Filosofiska Föreningen och Filosofiska Institutienen vid Uppsala Universitet, (1971).Google Scholar
[15] Solovay, R. M., Provability interpretations of modal logic, Israel Journal of Mathematics, vol. 28 (1976), pp. 33–71.Google Scholar