Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T17:17:00.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Models of set theory with more real numbers than ordinals

Published online by Cambridge University Press:  12 March 2014

Paul E. Cohen
Paul E. Cohen*
Affiliation:
Institute for Advanced Study, Princeton, New Jersey 08540
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose M is a countable standard transitive model of set theory. P. J. Cohen [2] showed that if κ is an infinite cardinal of M then there is a one-to-one function Fκ from κ into the set of real numbers such that M[Fκ] is a model of set theory with the same cardinals as M.

If Tκ is the range of Fκ then Cohen also showed [2] that M[Tκ] fails to satisfy the axiom of choice. We will give an easy proof of this fact.

If κ, λ are infinite we will also show that M[Tκ] is elementarily equivalent to M[Tλ] and that (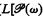] in M[Fλ]) is elementarily equivalent to (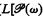] in M[FK]).

Finally we show that there may be an N ∈ M[GK] which is a standard model of set theory (without the axiom of choice) and which has, from the viewpoint of M[GK], more real numbers than ordinals.

We write ZFC and ZF for Zermelo-Fraenkel set theory, respectively with and without the axiom of choice (AC). GBC is Gödel-Bernays' set theory with AC. DC and ACℵo are respectively the axioms of dependent choice and of countable choice defined in [6].

Lower case Greek characters (other than ω) are used as variables over ordinals. When α is an ordinal, R(α) is the set of all sets with rank less than α.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 3 , September 1974 , pp. 579 - 583
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Cohen, P. E., Some applications of forcing in set theory, Doctoral Dissertation, University of Illinois, Champaign-Urbana, 1972.Google Scholar
[2]Cohen, P. J., Set theory and the continuum hypothesis, Benjamin, New York, 1966.Google Scholar
[3]Scott, D., Measurable cardinals and constructive sets, Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 7 (1961), pp. 145–149.Google Scholar
[4]Shoenfield, J., Unramified forcing, Proceedings of Symposia in Pure Mathematics, Vol. 13, Part 1 (University of California, Los Angeles, 1967), American Mathematical Society, Providence, R.I., 1971, pp. 357–381.Google Scholar
[5]Silver, J. H., Some applications of model theory in set Theory, Annals of Mathematical Logic, Vol. 3 (1971), pp. 45–110.CrossRefGoogle Scholar
[6]Takeuti, G., Hypotheses on power set, Proceedings of Symposia in Pure Mathematics, Vol. 13, Part 1 (University of California, Los Angeles, 1967), American Mathematical Society, Providence, R.I. 1971, pp. 439–446.Google Scholar
[7]Takeuti, G. and Zaring, W., Axiomatic set theory, Springer-Verlag, New York, 1973.CrossRefGoogle Scholar