Article contents
Minimal readability of intuitionistic arithmetic and elementary analysis
Published online by Cambridge University Press: 12 March 2014
Abstract
A new method of “minimal” readability is proposed and applied to show that the definable functions of Heyting arithmetic (HA)—functions f such that HA ⊢ ∀x∃!yA(x, y) ⇒ for all m, A(m, f(m)) is true, where A(x, y) may be an arbitrary formula of ℒ(HA) with only x,y free—are precisely the provably recursive functions of the classical Peano arithmetic (PA), i.e., the < ε0-recursive functions. It is proved that, for prenex sentences provable in HA, Skolem functions may always be chosen to be < ε0-recursive. The method is extended to intuitionistic finite-type arithmetic, 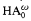 , and elementary analysis. Generalized forms of Kreisel's characterization of the provably recursive functions of PA and of the no-counterexample-interpretation for PA are consequently derived.
, and elementary analysis. Generalized forms of Kreisel's characterization of the provably recursive functions of PA and of the no-counterexample-interpretation for PA are consequently derived.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 6
- Cited by


