Published online by Cambridge University Press: 12 March 2014
In this paper we investigate the possibility of extending Friedberg's enumeration of the recursively enumerable (r.e.) sets without duplication [1, p. 312] to meta-recursion theory. It turns out that all of our proposed extensions are impossible save one: the metarecursively enumerable (meta-r.e.) sets can be enumerated without duplication, but only if all the recursive ordinals are used as indices (Theorems 1 and 2). The 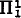 sets cannot be so enumerated, even if the index set is all recursive ordinals (Theorems 3 and 4). As a corollary, one proves there is no
sets cannot be so enumerated, even if the index set is all recursive ordinals (Theorems 3 and 4). As a corollary, one proves there is no 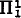 predicate P(n, x) with the property that for each
predicate P(n, x) with the property that for each 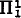 set A there is exactly one integer n for which A = {x ∣ P(n, x)}. We also discuss enumerations of nonempty, infinite, and coinfinite
set A there is exactly one integer n for which A = {x ∣ P(n, x)}. We also discuss enumerations of nonempty, infinite, and coinfinite 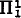 and meta-r.e. sets.
and meta-r.e. sets.