Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-07T17:32:11.023Z Has data issue: false hasContentIssue false
  • English
  • Français

A measure representation theorem for strong partition cardinals

Published online by Cambridge University Press:  12 March 2014

E. M. Kleinberg
E. M. Kleinberg*
Affiliation:
State University of New York, Buffalo, New York 14214
Get access Rights & Permissions [Opens in a new window]

Extract

There are two main axiomatic extensions of Zermelo-Fraenkel set theory without the axiom of choice, that associated with the axiom of determinateness, and that associated with infinite exponent partition relations. Initially, the axiom of determinateness, henceforth AD, was the sole tool available. Using it, set theorists in the late 1960s produced many remarkable results in pure set theory (e.g. the measurability of ℵ1) as well as in projective set theory (e.g. reduction principles for 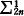). Infinite exponent partition relations were first studied successfully soon after these early consequences of AD. They too produced measurable cardinals and not only were the constructions here easier than those from AD—the results gave a far clearer picture of the measures involved than had been offered by AD. In general, the techniques offered by infinite exponent partition relations became so attractive that a great deal of the subsequent work from AD involved an initial derivation from AD of the appropriate infinite exponent partition relation and then the derivation from the partition relation of the desired result.

Since the early 1970s work on choiceless extensions of ZF + DC has split mainly between AD and its applications to projective set theory, and infinite exponent partition relations and their applications to pure set theory. There has certainly been a fair amount of interplay between the two, but for the most part the theories have been pursued independently.

Unlike AD, infinite exponent partition relations have shown themselves amenable to nontrivial forcing arguments. For example, Spector has constructed models for interesting partition relations, consequences of AD, in which AD is false. Thus AD is a strictly stronger assumption than are various infinite exponent partition relations. Furthermore, Woodin has recently proved the consistency of infinite exponent partition relations relative to assumptions consistent with the axiom of choice, in particular, relative to the existence of a supercompact cardinal. The notion of doing this for AD is not even considered.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 1 , March 1982 , pp. 161 - 168
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kechris, A., Kleinberg, E., Moschovakis, Y. and Woodin, H., The axiom of determinacy, strong partition relations, and non-singular measures, Cabal Seminar, 1977–79, Springer-Verlag (to appear).Google Scholar
[2]Kleinberg, E., Infinitary combinatorics and the axiom of determinateness, Lecture Notes in Mathematics, vol. 612, Springer-Verlag, Berlin and New York, 1977.Google Scholar
[3]Kleinberg, E., Strong partition properties for infinite cardinals, this Journal, vol. 35 (1970), pp. 410–428.Google Scholar
[4]Kleinberg, E., AD ⊢ “the ℵn are Jonsson cardinals and ℵω is a Rowbottom cardinal”, Annals of Mathematical Logic, vol. 12 (1977), pp. 229–248.CrossRefGoogle Scholar
[5]Kleinberg, E., Producing measurable cardinals beyond k, this Journal, vol. 46 (1981), pp. 643–648.Google Scholar
[6]Martin, D.A. and Paris, J.B., AD⇒∃ exactly 2 normal measures on ω2, circulated note, 03 1971.Google Scholar
[7]Martin, D.A., The axiom of determinateness and reduction principles in the analytical hierarchy, Bulletin of the American Mathematical Society, vol. 74 (1968), pp. 687–689.CrossRefGoogle Scholar
[8]Addison, J.W. and Moschovakis, Y.N., Some consequences of the axiom of definable determinateness, Proceedings of the National Academy of Sciences of the United States of America, vol. 59 (1968), pp. 708–712.CrossRefGoogle ScholarPubMed
[9]Solovay, R.M., Measurable cardinals and the axiom of determinateness, lecture notes prepared in connection with the Summer Institute on Axiomatic Set Theory, University of California, Los Angeles, 1967.Google Scholar