Article contents
Meager sets on the hyperfinite time line
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we study notions of a “meager subset” of a hyper-finite set. We work within an ω-saturated nonstandard universe and fix a hyperfinite natural number 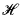 Є *N∖N. We shall consider subsets of the set
Є *N∖N. We shall consider subsets of the set 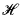 = {1, 2, …,H}.
= {1, 2, …,H}.
By analogy with the meager subsets of the real interval [0, 1], a notion of meager subset of 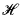 should have the following properties.
should have the following properties.
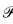 1. Finite sets, countable unions of meager sets, subsets of meager sets, and translates of meager sets should be meager.
1. Finite sets, countable unions of meager sets, subsets of meager sets, and translates of meager sets should be meager.
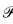 2. The Baire Category Theorem should hold; that is,
2. The Baire Category Theorem should hold; that is, 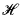 should not be meager.
should not be meager.
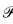 3. The internal analogue of the Cantor set should be meager.
3. The internal analogue of the Cantor set should be meager.
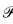 4. The notion of a meager set should be with respect to a natural topology on
4. The notion of a meager set should be with respect to a natural topology on 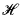 .
.
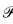 5. There should exist meager subsets of
5. There should exist meager subsets of 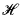 of Loeb measure one.
of Loeb measure one.
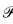 6. Sierpiński and Lusin sets should have hyperfinite counterparts with properties similar to the classical case.
6. Sierpiński and Lusin sets should have hyperfinite counterparts with properties similar to the classical case.
Property 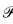 5 is desirable so that, as with Lebesgue measure and Baire category on [0, 1], the topological and measure-theoretic notions of “large” and “small” sets are incomparable.
5 is desirable so that, as with Lebesgue measure and Baire category on [0, 1], the topological and measure-theoretic notions of “large” and “small” sets are incomparable.
Property 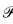 6, while not as necessary as the other five, is desirable because of the strong interplay between measure and category in the classical results about Lusin and Sierpinski sets. Our objective is to find notions of meager set which have a relationship to Loeb measure similar to the classical relationship between meager sets and Lebesgue measure.
6, while not as necessary as the other five, is desirable because of the strong interplay between measure and category in the classical results about Lusin and Sierpinski sets. Our objective is to find notions of meager set which have a relationship to Loeb measure similar to the classical relationship between meager sets and Lebesgue measure.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991
References
REFERENCES
- 13
- Cited by


