Article contents
Maximal and Cohesive vector spaces1
Published online by Cambridge University Press: 12 March 2014
Extract
Let N denote the natural numbers. If A ⊆ N, we write Ā for the complement of A in N. A set A ⊆ N is cohesive if (i) A is infinite and (ii) for any recursively enumerable set W either W ∩ A or 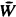 ∩ A is finite. A r.e. set M ⊆ N is maximal if
∩ A is finite. A r.e. set M ⊆ N is maximal if 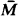 is cohesive.
is cohesive.
A recursively presented vector space (r.p.v.s.) U over a recursive field F consists of a recursive set U ⊆ N and operations of vector addition and scalar multiplication which are partial recursive and under which U becomes a vector space. A r.p.v.s. U has a dependence algorithm if there is a uniform effective procedure which applied to any n-tuple ν0, ν1, …, νn−1 of elements of U determines whether or not ν0, ν1 …, νn−1 are linearly dependent. Throughout this paper we assume that if U is a r.p.v.s. over a recursive field F then U is infinite dimensional and U = N. If W ⊆ U, then we say W is recursive (r.e., etc.) iff W is a recursive (r.e., etc.) subset of N. If S ⊆ U, we write (S)* for the subspace generated by S. If V1 and V2 are subspaces of U such that V1 ∩ V2 ={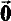 } (where
} (where 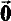 is the zero vector of U), then we write V1 ⊕ V2 for (V1 ∪ V2)*. If V1 ⊆ V2⊆U are subspaces, we write V2/V1 for the quotient space.
is the zero vector of U), then we write V1 ⊕ V2 for (V1 ∪ V2)*. If V1 ⊆ V2⊆U are subspaces, we write V2/V1 for the quotient space.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977
Footnotes
We wish to acknowledge valuable conversations with A. Nerode and G. Metakides.
References
REFERENCES
- 13
- Cited by


