No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
We start with the framework upon which this paper is based. The most useful reference for these notions is [2]. For any nonempty index set I and any proper filter D on S(I) (the power set of I), we denote by 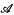 I/D the reduced power of
I/D the reduced power of 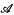 modulo D as defined in [2, pp. 167–169]. The first-order language associated with
modulo D as defined in [2, pp. 167–169]. The first-order language associated with 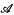 I/D will always be the same language as associated with
I/D will always be the same language as associated with 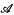 . We denote the 2-element Boolean algebra 〈{0, 1}, ⋂, ⋃, c, 0, 1〉 by 2 and 2I/D denotes the reduced power of it modulo D. We point out the intimate connection between the structures
. We denote the 2-element Boolean algebra 〈{0, 1}, ⋂, ⋃, c, 0, 1〉 by 2 and 2I/D denotes the reduced power of it modulo D. We point out the intimate connection between the structures 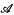 I/D and 2I/D given in [2, pp. 341–345]. Moreover, we assume as known the definition of Horn formula and Horn sentence as given in [2, p. 328] along with the fundamental theorem that φ is a reduced product sentence iff φ is provably equivalent to a Horn sentence [2, Theorem 6.2.5/ (iff φ is a 2-direct product sentence and a reduced power sentence [2, Proposition 6.2.6(ii)]). For a theory T(any set of sentences),
I/D and 2I/D given in [2, pp. 341–345]. Moreover, we assume as known the definition of Horn formula and Horn sentence as given in [2, p. 328] along with the fundamental theorem that φ is a reduced product sentence iff φ is provably equivalent to a Horn sentence [2, Theorem 6.2.5/ (iff φ is a 2-direct product sentence and a reduced power sentence [2, Proposition 6.2.6(ii)]). For a theory T(any set of sentences), 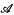 ⊨ T denotes that
⊨ T denotes that 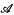 is a model of T.
is a model of T.
In addition to the above we assume as known the elementary characteristics (due to Tarski) associated with a complete theory of a Boolean algebra, and we adopt the notation 〈n, p, q〉 of [3], [10], or [6] to denote such an elementary characteristic or the corresponding complete theory. We frequently will use Ershov's theorem which asserts that for each 〈n, p, q〉 there exist an index set I and filter D such that 2I/D ⊨ 〈n, p, q〉 [3] or [2, Lemma 6.3.21].