Article contents
Local Kc constructions
Published online by Cambridge University Press: 12 March 2014
Extract
The full-background-extender Kc -construction of [2] has the property that, if it does not break down and produces a final model 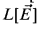 , then
, then
Ή is Woodin in V ⇒ Ή is Woodin in 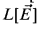 ,
,
for all Ή. It is natural to ask whether
κ is strong in V ⇒ κ is λ-strong in 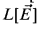 ,
,
for all κ, or even better,
κ is λ-strong in V ⇒ κ is λ-strong in 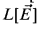 .
.
As one might suspect, the more useful answer would be “yes”.
For the Kc-construction of [2], this question is open. The problem is that the construction of [2] is not local: because of the full-background-extender demand, it may produce mice projecting to ρ at stages much greater than ρ. Because of this, there is no reason to believe that if E is a λ-strong extender of V, then 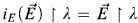 The natural proof only gives that if κ is Σ2-strong, then Σ, is strong in
The natural proof only gives that if κ is Σ2-strong, then Σ, is strong in 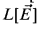 .
.
We do not know how to get started on this question, and suspect that in fact strong cardinals in V may fail to be strong in 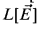 , if
, if 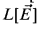 is the output of the construction of [2]. Therefore, we shall look for a modification of the construction of [2]. One might ask for a construction with output
is the output of the construction of [2]. Therefore, we shall look for a modification of the construction of [2]. One might ask for a construction with output 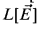 such that
such that
(1) iteration trees on 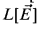 can be lifted to iteration trees on V,
can be lifted to iteration trees on V,
(2) ∀δ(δ is Woodin ⇒ δ is Woodin in 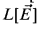 ), and
), and
(3) (a) ↾κ(κ is a strong cardinal ⇒ κ is strong in 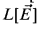 ), and (b) ↾κ↾λ(Lim(λ) Λ κ is λ-strong ⇒ κ is λ-strong in
), and (b) ↾κ↾λ(Lim(λ) Λ κ is λ-strong ⇒ κ is λ-strong in 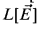 ).
).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2007
References
- 4
- Cited by


