Article contents
A LIGHTFACE ANALYSIS OF THE DIFFERENTIABILITY RANK
Published online by Cambridge University Press: 17 April 2014
Abstract
We examine the computable part of the differentiability hierarchy defined by
Kechris and Woodin. In that hierarchy, the rank of a differentiable function is
an ordinal less than 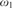 ${\omega _1}$ which measures how complex it is to verify differentiability
for that function. We show that for each recursive ordinal
${\omega _1}$ which measures how complex it is to verify differentiability
for that function. We show that for each recursive ordinal 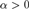 $\alpha > 0$, the set of Turing indices of
$\alpha > 0$, the set of Turing indices of 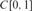 $C[0,1]$ functions that are differentiable with rank at most
α is
$C[0,1]$ functions that are differentiable with rank at most
α is 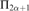 ${{\rm{\Pi }}_{2\alpha + 1}}$-complete. This result is expressed in the notation of Ash and
Knight.
${{\rm{\Pi }}_{2\alpha + 1}}$-complete. This result is expressed in the notation of Ash and
Knight.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2014
References
REFERENCES
- 3
- Cited by


