Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T18:06:09.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice embeddings into the recursively enumerable degrees. II

Published online by Cambridge University Press:  12 March 2014

K. Ambos-Spies  and
M. Lerman
K. Ambos-Spies*
Affiliation:
Lehrstuhl Informatik II, Universität Dortmund, D-4600 Dortmund 50, West Germany
M. Lerman
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, Connecticut 06269
*
Mathematisches Institut, Universität Heidelberg, D-6900 Heidelberg 1, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

The problem of characterizing the finite lattices which can be embedded into the recursively enumerable degrees has a long history, which is summarized in [AL]. This problem is an important one, as its solution is necessary if a decision procedure for the ∀∃-theory of the poset 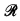of recursively emumerable degrees is to be found. A recursive nonembeddability condition, NEC, which subsumes all known nonembeddability conditions was presented in [AL]. This paper focuses on embeddability. An embeddability condition, EC, is introduced, and we prove that every finite lattice having EC can be embedded (as a lattice) into 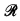. EC subsumes all known embeddability conditions.

EC is a Π3 condition which states that certain obstructions to proving embeddability do not exist. It seems likely that the recursive labeled trees used in EC can be replaced with trees which are effectively generated from uniformly defined finite trees, in which case EC would be equivalent to a recursive condition. We do not know whether EC and NEC are complementary. This problem seems to be combinatorial, rather than recursion-theoretic in nature. Our efforts to find a finite lattice satisfying neither EC nor NEC have, to this point, been unsuccessful. It is the second author's conjecture that the techniques for proving embeddability which are used in this paper cannot be refined very much to obtain new embeddability results.

EC is introduced in §2, and the various conditions and definitions are motivated by presenting examples of embeddable lattices and indicating how the embedding proof works in those particular cases. The embedding construction is presented in §3, and the proof in §4.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 735 - 760
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AL]Ambos-Spies, K. and Lerman, M., Lattice embeddings into the recursively enumerable degrees, this Journal, vol. 51 (1986), pp. 257–272.Google Scholar
[EP]Epstein, R. L. and Posner, D., Diagonalization in degree constructions, this Journal, vol. 43 (1978), pp. 280–283.Google Scholar
[La]Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceedings of the London Mathematical Society, ser. 3, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[La2]Lachlan, A. H., Embedding nondistributive lattices into the recursively enumerable degrees, Conference in mathematical logic—London 1970, Lecture Notes in Mathematics, vol. 255, Springer-Verlag, 1972, pp. 149–177.Google Scholar
[LaSo]Lachlan, A. H. and Soare, R. I., Not every finite lattice is embeddable in the recursively enumerable degrees, Advances in Mathematics, vol. 37 (1980), pp. 74–82.CrossRefGoogle Scholar
[Le]Lerman, M., Admissible ordinals and priority arguments, Proceedings of the Cambridge summer school in logic 1971, Lecture Notes in Mathematics, vol. 337, Springer-Verlag, Berlin, 1973, pp. 311–344.Google Scholar
[LSS]Lerman, M., Shore, R. A. and Soare, R. I., The elementary theory of the recursively enumerable degrees is not ℵ0-categorical, Advances in Mathematics, vol. 53 (1984), pp. 301–320.CrossRefGoogle Scholar
[S]Sacks, G. E., Degrees of unsohability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, New Jersey, 1963.Google Scholar
[T]Thomason, S. K., Sublattices of the recursively enumerable degrees, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 17 (1971), pp. 273–280.CrossRefGoogle Scholar
[Y]Yates, C. E. M., A minimal pair of recursively enumerable degrees, this Journal, vol. 31 (1966), pp. 159–168.Google Scholar