Article contents
Large families of incomparable A-isols
Published online by Cambridge University Press: 12 March 2014
Extract
The set Λ of isols was extensively studied by Dekker and Myhill in [1]. Subsequently, Nerode [3] developed the theory of Λ(A), the set of isols relative to some recursively closed set of functions A.
One of the main areas of interest of [1] was the natural partial order ≤ on Λ. In this paper we will examine some of the properties of ≤A on Λ(A). We use the following notations: ∣A∣ is the cardinality of the set A, ⊃ denotes strict inclusion, 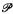 (a) is the power set of the set a, c is the cardinality of the continuum, and ω = {0, 1, 2, …}. The terms A-isol, A-immune, A-r.e., A-incomparable, etc. all refer to the usual meaning of these words, only taken in the context of the recursively closed set A. ReqA(a) is the A-r.e.t. of which a is a representative. By identifying a finite natural number with the A-r.e.t. consisting of sets of a given finite cardinality we see that ω ⊆ Λ(A); Λ(A) is said to be nontrivial iff ω ⊃ Λ(A). The three results proven in this paper are:
(a) is the power set of the set a, c is the cardinality of the continuum, and ω = {0, 1, 2, …}. The terms A-isol, A-immune, A-r.e., A-incomparable, etc. all refer to the usual meaning of these words, only taken in the context of the recursively closed set A. ReqA(a) is the A-r.e.t. of which a is a representative. By identifying a finite natural number with the A-r.e.t. consisting of sets of a given finite cardinality we see that ω ⊆ Λ(A); Λ(A) is said to be nontrivial iff ω ⊃ Λ(A). The three results proven in this paper are:
Theorem 1. If Λ(A) is nontrivial, then ∣Λ(A)∣ = c.
Theorem 2. If∣A∣ < c, then Λ(A) is nontrivial.
Theorem 3. If ∣A∣ < c and ∣⊿∣ < c and ⊿ ⊆ Λ(A) − ω, then there is aΓ ⊆ Λ(A) − ω such that:
(a) ∣Γ∣ = c.
(b) Every member of Γ is A-incomparable with every member of Δ.
(c) Any two distinct members of Γ are A-incomparable.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 1
- Cited by


