Article contents
LARGE CARDINALS AND LIGHTFACE DEFINABLE WELL-ORDERS, WITHOUT THE GCH
Published online by Cambridge University Press: 13 March 2015
Abstract
This paper deals with the question whether the assumption that for every inaccessible cardinal κ there is a well-order of H(κ+) definable over the structure 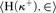 $\langle {\rm{H}}({\kappa ^ + }), \in \rangle$ by a formula without parameters is consistent with the existence of (large) large cardinals and failures of the GCH. We work under the assumption that the SCH holds at every singular fixed point of the ℶ-function and construct a class forcing that adds such a well-order at every inaccessible cardinal and preserves ZFC, all cofinalities, the continuum function, and all supercompact cardinals. Even in the absence of a proper class of inaccessible cardinals, this forcing produces a model of “V = HOD” and can therefore be used to force this axiom while preserving large cardinals and failures of the GCH. As another application, we show that we can start with a model containing an ω-superstrong cardinal κ and use this forcing to build a model in which κ is still ω-superstrong, the GCH fails at κ and there is a well-order of H(κ+) that is definable over H(κ+) without parameters. Finally, we can apply the forcing to answer a question about the definable failure of the GCH at a measurable cardinal.
$\langle {\rm{H}}({\kappa ^ + }), \in \rangle$ by a formula without parameters is consistent with the existence of (large) large cardinals and failures of the GCH. We work under the assumption that the SCH holds at every singular fixed point of the ℶ-function and construct a class forcing that adds such a well-order at every inaccessible cardinal and preserves ZFC, all cofinalities, the continuum function, and all supercompact cardinals. Even in the absence of a proper class of inaccessible cardinals, this forcing produces a model of “V = HOD” and can therefore be used to force this axiom while preserving large cardinals and failures of the GCH. As another application, we show that we can start with a model containing an ω-superstrong cardinal κ and use this forcing to build a model in which κ is still ω-superstrong, the GCH fails at κ and there is a well-order of H(κ+) that is definable over H(κ+) without parameters. Finally, we can apply the forcing to answer a question about the definable failure of the GCH at a measurable cardinal.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
- 1
- Cited by


