Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T10:56:59.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Interpreting true arithmetic in the 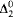-enumeration degrees

Published online by Cambridge University Press:  12 March 2014

Thomas F. Kent
Thomas F. Kent*
Affiliation:
Department of Mathematics, Marywood University, 2300 Adams Avenue, Scranton, Pa 18509, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

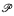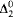We show that there is a first order sentence φ(x: a, b, l) such that for every computable partial order and -degree u > 0e, there are 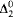-enumeration degrees a ≤ u, b, and l such that 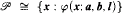. Allowing 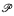to be a suitably defined standard model of arithmetic gives a parameterized interpretation of true arithmetic in the 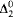-enumeration degrees. Finally we show that there is a first order sentence that correctly identifies a subset of the standard models, which gives a parameterless interpretation of true arithmetic in the 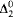-enumeration degrees.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 2 , June 2010 , pp. 522 - 550
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Affitato, M. L., Kent, T. F., and Sorbi, A., Undecidability of local structures of s-degrees and Q-degrees, Tbilisi Mathematical Journal, to appear.Google Scholar
[2]Ahmad, S., Some results on enumeration reducibility, Ph.D. thesis, Simon Frasier University, 1989.Google Scholar
[3]Ahmad, S., Embedding the diamond in the Σ20 enumeration degrees, this Journal, vol. 56 (1991), no. 1, pp. 195–212.Google Scholar
[4]Ahmad, S. and Lachlan, A. H., Some special pairs Σ20 e-degrees, Mathematical Logic Quarterly, vol. 44 (1998), no. 4, pp. 431–449.CrossRefGoogle Scholar
[5]Arslanov, M. M.. Kalimullin, I. Sh., and Sorbi, A., Density results in the Δ20 e-degrees, Archive for Mathematical Logic, vol. 40 (2001), no. 8, pp. 597–614.CrossRefGoogle Scholar
[6]Case, J., Enumeration reducibility and partial degrees, Archive for Mathematical Logic, vol. 2 (1971), pp. 419–439.CrossRefGoogle Scholar
[7]Cooper, S. B., Partial degrees and the density problem, part II: The enumeration degrees of the Σ20-sets are dense, this Journal, vol. 49 (1984), no. 2, pp. 503–513.Google Scholar
[8]Cooper, S. B., Enumeration reducibility, nondeterministic computations and relative computability of partial functions, Recursion theory week (Oberwolfach, 1989), Lecture Notes in Mathematics, vol. 1432, Springer, Berlin, 1990, pp. 57–110.CrossRefGoogle Scholar
[9]Downey, R. G., Laforte, G., and Nies, A., Computably enumerable sets and quasi-reducibility, Annals of Pure and Applied Logic, vol. 95 (1998), no. 1-3, pp. 1–35.CrossRefGoogle Scholar
[10]Harrington, L. and Nies, A., Coding in the partial order of enumerable sets, Advances in Mathematics, vol. 133 (1998), no. 1, pp. 133–162.CrossRefGoogle Scholar
[11]Kent, T. F., The Π3-theory of the Σ20-enumeration degrees is undecidable, this Journal, vol. 71 (2006), no. 4, pp. 1284–1302.Google Scholar
[12]Lachlan, A. H., Lower bounds for pairs of recursively enumerable degrees, Proceedings of the London Mathematical Society, vol. 16 (1966), pp. 537–569.CrossRefGoogle Scholar
[13]Lachlan, A. H. and Shore, R., The n-rea enumeration degrees are dense, Archive for Mathematical Logic, vol. 31 (1992), no. 4, pp. 277–285.CrossRefGoogle Scholar
[14]Lempp, S., Slaman, T., and Sorbi, A., On extensions of emheddings into the enumeration degrees of the Σ20-sets, Journal of Mathematical Logic, vol. 5 (2005), no. 2, pp. 247–298.CrossRefGoogle Scholar
[15]Lempp, S. and Sorbi, A., Embedding finite lattices into the Σ20 enumeration degrees, this Journal, vol. 67 (2002), no. 1, pp. 69–90.Google Scholar
[16]Mcevoy, K., Jumps of quasi-minimal enumeration degrees, this Journal, vol. 50 (1985), no. 3, pp. 839–848.Google Scholar
[17]McEvoy, K. and Cooper, S. B., On minimal pairs of enumeration-degrees, this Journal, vol. 50 (1985), no. 4, pp. 839–848.Google Scholar
[18]Medvedev, Y., Degrees of difficulty of the mass problem, Doklady Akademii Nauk SSSR (N.S.), vol. 104 (1955), pp. 501–504.Google Scholar
[19]Nies, A., Definability and undecidability in recursion theoretic semilattices, Ph.D. thesis, Ruprecht-Kals-Universität Heidelberg, 1994.Google Scholar
[20]Nies, A., The last question on recursively enumerable m-degrees, Sibirskiĭ Fond Algebry i Logiki. Algebra i Logika, vol. 33 (1994), no. 5, pp. 550–563, 597.Google Scholar
[21]Nies, A., Undecidable fragments of elementary theories, Algebra Universalis, vol. 35 (1996). no. 1, pp. 8–33.CrossRefGoogle Scholar
[22]Nies, A., Interpreting N in the computably enumerable weak truth table degrees, Annals of Pure and Applied Logic, vol. 107 (2001), no. 1-3, pp. 35–48.CrossRefGoogle Scholar
[23]Nies, A. and Shore, R. A., Interpreting true arithmetic in the theory of the r.e. truth table degrees, Annals of Pure and Applied Logic, vol. 75 (1995), no. 3, pp. 269–311.CrossRefGoogle Scholar
[24]Nies, A., Shore, R. A., and Slaman, T., Interpretability and definability in the recursively enumerable degrees, Proceedings of the London Mathematical Society. Third Series, vol. 77 (1998), no. 2, pp. 241–291.CrossRefGoogle Scholar
[25]Sacks, G. E., On the degrees less than 0′, Annals of Mathematics, vol. 77 (1963), pp. 211–231.CrossRefGoogle Scholar
[26]Shore, R. A., The theory of the degrees below 0′, The Journal of the London Mathematical Society. Second Series, vol. 24 (1981), no. 1, pp. 1–14.CrossRefGoogle Scholar
[27]Simpson, S. G., First-order theory of the degrees of recursive unsolvability, Annals of Mathematics. Second Series, vol. 105 (1977), no. 1, pp. 121–139.CrossRefGoogle Scholar
[28]Slaman, T. and Woodin, W., Definability in the enumeration degrees, Archive for Mathematical Logic, vol. 36 (1997), no. 4-5, pp. 255–267.CrossRefGoogle Scholar
[29]Soare, R. I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
[30]Sorbi, A., The enumeration degrees of the Σ20 sets, Complexity, logic, and recursion theory, Lecture Notes in Pure and Applied Mathematics, vol. 187, Dekker, New York, 1997, pp. 303–330.Google Scholar
[31]Sorbi, A., Open problems in the enumeration degrees, Computability theory and its applications (Boulder, CO, 1999), Contemp. Math., vol. 257, Amer. Math. Soc, Providence, RI, 2000, pp. 309–320.CrossRefGoogle Scholar