This paper addresses the structures (M, ω) and (ω, SSy(M)), where M is a nonstandard model of PA and ω is the standard cut. It is known that (ω, SSy(M)) is interpretable in (M, ω). Our main technical result is that there is an reverse interpretation of (M, ω) in (ω, SSy(M)) which is ‘local’ in the sense of Visser [11]. We also relate the model theory of (M, ω) to the study of transplendent models of PA [2].

This yields a number of model theoretic results concerning the ω-models (M, ω) and their standard systems SSy(M, ω), including the following.

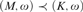• $\left( {M,\omega } \right) \prec \left( {K,\omega } \right)$ if and only if 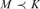$M \prec K$ and 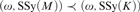$\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\rm{SSy}}\left( K \right)} \right)$.

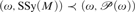• $\left( {\omega ,{\rm{SSy}}\left( M \right)} \right) \prec \left( {\omega ,{\cal P}\left( \omega \right)} \right)$ if and only if 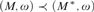$\left( {M,\omega } \right) \prec \left( {{M^{\rm{*}}},\omega } \right)$ for some ω-saturated M*.

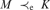• $M{ \prec _{\rm{e}}}K$ implies SSy(M, ω) = SSy(K, ω), but cofinal extensions do not necessarily preserve standard system in this sense.

• SSy(M, ω)=SSy(M) if and only if (ω, SSy(M)) satisfies the full comprehension scheme.

• If SSy(M, ω) is uniformly defined by a single formula (analogous to a β function), then (ω, SSy(M, ω)) satisfies the full comprehension scheme; and there are models M for which SSy(M, ω) is not uniformly defined in this sense.