No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
In Barwise and van Benthem [6], the authors give a general method for obtaining interpolation and preservation theorems for fragments of L∞ω, those for which there is a co-inductive pebble game Γ characterizing equivalence in the logic. The method is exemplified by an analysis of the following fragments: L∞ω itself, its existential fragment 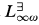 , its positive fragment
, its positive fragment 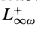 , the k-variable fragment
, the k-variable fragment 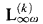 (and its existential and positive subfragments) and the modal fragment
(and its existential and positive subfragments) and the modal fragment 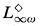 (and its existential and positive subfragments).
(and its existential and positive subfragments).
While most of their method is general, there is one part (showing that Γ has the Scott property relative to the fragment) that required a case-by-case analysis. The purpose of our paper is to replace this case-by-case analysis by a general theorem, and to illustrate this method by obtaining their kinds of results for some additional fragments of L∞ω.
Our general problem can be stated in the following way: Given a “nice” fragment F of L∞ω (one satisfying some natural closure conditions), find a pebble game characterization Γ of “preservation of F-formulas” and prove that Γ has the Scott property with respect to F. Applying the Abstract Interpolation Theorem from [6], we can conclude that F has Γ-interpolation, and the corresponding preservation result. In this paper, we shall give an answer to this question. (Our answer is “sufficient” but we don't know if our conditions are necessary.)