In this paper we continue the study of inner models of the type studied in Inner models for set theory—Part I. The present paper is concerned exclusively with a particular kind of model, the ‘super-complete models’ defined in section 2.4 of I (page 186). The condition (c) of 2.4 and the completeness condition 1.42 imply that such a model is uniquely determined when its universal class Vm is given. Writing condition (c) and the completeness conditions 1.41, 1.42 in terms of Vm , we may state the definition in the form:

3.1. Dfn. A class Vm is said to determine a super-complete model if the model whose basic notions are defined by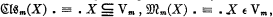, 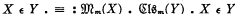satisfies axioms A, B, C.

N. B. This definition is not necessarily metamathematical in nature. If desired, it could be written out quite formally as the definition of a notion ‘SCM(U)’ (‘U determines a super-complete model’) thus:

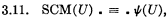
where ψ(U) is the propositional function expressing in terms of U the fact that the model determined by U according to 3.1 satisfies the relativization of axioms A, B, C. E.g. corresponding to axiom A1m , i.e., 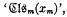, ψ(U) contains the equivalent term 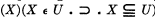. All the relativized axioms can be similarly expressed in this way by first writing out the relativized form (after having replaced all defined symbols which occur by the corresponding formulae in primitive notation) and then replacing ‘(A m )ϕ(A m ) by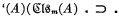 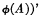which is in turn replaced by 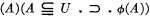, and similarly replacing ‘(xm )ϕ(xm )’ by ‘(x m )ϕ(x m )’ by ‘(X)(X ϵ U ▪ ⊃ ▪ ϕ (X)), and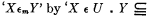 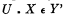Thus ψ(U) is obtained in primitive notation.