No CrossRef data available.
Article contents
INFINITE STRINGS AND THEIR LARGE SCALE PROPERTIES
Published online by Cambridge University Press: 30 October 2020
Abstract
The aim of this paper is to shed light on our understanding of large scale properties of infinite strings. We say that one string 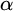 $\alpha $
has weaker large scale geometry than that of
$\alpha $
has weaker large scale geometry than that of 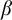 $\beta $
if there is color preserving bi-Lipschitz map from
$\beta $
if there is color preserving bi-Lipschitz map from 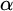 $\alpha $
into
$\alpha $
into 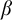 $\beta $
with small distortion. This definition allows us to define a partially ordered set of large scale geometries on the classes of all infinite strings. This partial order compares large scale geometries of infinite strings. As such, it presents an algebraic tool for classification of global patterns. We study properties of this partial order. We prove, for instance, that this partial order has a greatest element and also possess infinite chains and antichains. We also investigate the sets of large scale geometries of strings accepted by finite state machines such as Büchi automata. We provide an algorithm that describes large scale geometries of strings accepted by Büchi automata. This connects the work with the complexity theory. We also prove that the quasi-isometry problem is a
$\beta $
with small distortion. This definition allows us to define a partially ordered set of large scale geometries on the classes of all infinite strings. This partial order compares large scale geometries of infinite strings. As such, it presents an algebraic tool for classification of global patterns. We study properties of this partial order. We prove, for instance, that this partial order has a greatest element and also possess infinite chains and antichains. We also investigate the sets of large scale geometries of strings accepted by finite state machines such as Büchi automata. We provide an algorithm that describes large scale geometries of strings accepted by Büchi automata. This connects the work with the complexity theory. We also prove that the quasi-isometry problem is a  $\Sigma _2^0$
-complete set, thus providing a bridge with computability theory. Finally, we build algebraic structures that are invariants of large scale geometries. We invoke asymptotic cones, a key concept in geometric group theory, defined via model-theoretic notion of ultra-product. Partly, we study asymptotic cones of algorithmically random strings, thus connecting the topic with algorithmic randomness.
$\Sigma _2^0$
-complete set, thus providing a bridge with computability theory. Finally, we build algebraic structures that are invariants of large scale geometries. We invoke asymptotic cones, a key concept in geometric group theory, defined via model-theoretic notion of ultra-product. Partly, we study asymptotic cones of algorithmically random strings, thus connecting the topic with algorithmic randomness.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



