Article contents
Indescribable cardinals and elementary embeddings
Published online by Cambridge University Press: 12 March 2014
Extract
Indescribability is closely related to the reflection principles of Zermelo-Fränkel set theory. In this axiomatic setting the universe of all sets stratifies into a natural cumulative hierarchy (Vα: α ϵ On) such that any formula of the language for set theory that holds in the universe already holds in the restricted universe of all sets obtained by some stage.
The axioms of ZF prove the existence of many ordinals α such that this reflection scheme holds in the world Vα. Hanf and Scott noticed that one arrives at a large cardinal notion if the reflecting formulas are allowed to contain second order free variables to which one assigns subsets of Vα. For a given collection Ω of formulas in the ϵ language of set theory with higher type variables and a unary predicate symbol they define an ordinal α to be Ω indescribable if for all sentences Φ in Ω and A ⊆ Vα
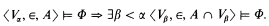
Since a sufficient coding apparatus is available, this definition is (for the classes of formulas that we are going to consider) equivalent to the one that one obtains by allowing finite sequences of relations over Vα, some of which are possibly k-ary. We will be interested mainly in certain standardized classes of formulas: Let 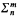 (
(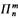 , respectively) denote the class of all formulas in the language introduced above whose prenex normal form has n alternating blocks of quantifiers of type m (i.e. (m + 1)th order) starting with ∃ (∀, respectively) and no quantifiers of type greater than m. In Hanf and Scott [1961] it is shown that in ZFC,
, respectively) denote the class of all formulas in the language introduced above whose prenex normal form has n alternating blocks of quantifiers of type m (i.e. (m + 1)th order) starting with ∃ (∀, respectively) and no quantifiers of type greater than m. In Hanf and Scott [1961] it is shown that in ZFC, 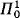 indescribability is equivalent to inaccessibility and
indescribability is equivalent to inaccessibility and 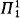 indescribability coincides with weak compactness.
indescribability coincides with weak compactness.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1991
References
REFERENCES
- 22
- Cited by


