Article contents
The implicational fragment of Dummett's LC
Published online by Cambridge University Press: 12 March 2014
Extract
It has been shown in Dummett [1] that the system LC given by Heyting's Calculus plus the additional axiom ACpqCqp is complete with respect to the model having as truth values the integers 0, 1,2, … and ω, 0 being the designated value, with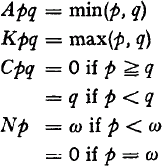
In this system CCCpqrCCCqprr is equivalent to ACpqCqp, and the purpose of this paper is to show that the implicational fragment of Heyting's Calculus plus the additional axiom CCCpqrCCCqprr yields the implicational fragment of LC.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1962
References
[1]Dummett, Michael, A prepositional calculus with denumerable matrix, this Journal, vol. 24 (1959) pp. 96–107.Google Scholar
[2]Prior, A. N., Logicians at play; or Syll, Simp and Hilbert, Australasian Journal of Philosophy, vol. 34 (1956), pp. 182–192.CrossRefGoogle Scholar
- 10
- Cited by


