In [1] Diego showed that there are only finitely many nonequivalent formulas in n variables in the positive implicational propositional calculus P. He also gave a recursive construction of the corresponding algebra of formulas, the free Hilbert algebra In on n free generators. In the present paper we give an alternative proof of the finiteness of In, and another construction of free Hilbert algebras, yielding a normal form for implicational formulas. The main new result is that In is built up from n copies of a finite Boolean algebra. The proofs use Kripke models [2] rather than the algebraic techniques of [1].

Let V be a finite set of propositional variables, and let F(V) be the set of all formulas built up from V ⋃ {t} using → alone. The algebra defined on the equivalence classes 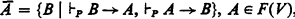, by setting

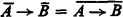
is a free Hilbert algebra I(V) on the free generators 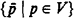. A set T ⊆ F(V) is a theory if ⊦pA implies A ∈ T, and T is closed under modus ponens. For T a theory, T[A] is the theory {B ∣ A → B ∈ T}. A theory T is p-prime, where p ∈ V, if p ∉ T and, for any A ∈ F(V), A ∈ T or A → p ∈ T. A theory is prime if it is p-prime for some p. Pp(V) denotes the set of p-prime theories in F(V), P(V) the set of prime theories. T ∈ P(V) is minimal if there is no theory in P(V) strictly contained in T. Where X = {A1, …, An} is a finite set of formulas, let X → B be A1 →····→·An → B (ϕ → B is B). A formula A is a p-formula if p is the right-most variable occurring in A, i.e. if A is of the form X → p.