No CrossRef data available.
Article contents
Hyperhypersimple supersets in admissible recursion theory
Published online by Cambridge University Press: 12 March 2014
Extract
Let α be an admissible ordinal. An α-recursively enumerable set H is hyper-hypersimple (hh-simple) if its lattice of α-r.e. supersets forms a Boolean algebra. In [3], Chong and Lerman characterized the class ℋ(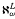 ) of hh-simple
) of hh-simple 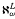 -r.e. sets as precisely those
-r.e. sets as precisely those 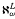 -r.e. sets whose complements are unbounded and of order type less than
-r.e. sets whose complements are unbounded and of order type less than 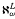 . Perhaps a nice example of such a set is {σ∣σ is not
. Perhaps a nice example of such a set is {σ∣σ is not 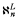 for any n < ω}. It follows that all hh-simple sets in
for any n < ω}. It follows that all hh-simple sets in 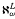 are nonhyperregular and therefore of degree 0′. That ℋ(
are nonhyperregular and therefore of degree 0′. That ℋ(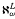 ) is a natural class to study can be seen from the role played by its ω-counterpart in the study of decision problems and automorphisms of ℰ*(ω), the lattice of ω-r.e. sets modulo finite sets (Soare [13] gives an extensive literature on these topics). In α-recursion theory the existence of hh-simple sets is not an all pervasive phenomenon, and there is as yet no complete characterization of the admissible ordinal α for which ℋ(α) is nonempty. While this situation is admittedly unsatisfactory, we feel that the lattice ℰ*(α) of α-r.e. sets modulo α*-finite sets for which ℋ(α) ≠ ∅ deserves a careful study. Indeed armed with some understanding over the last few years of the general theory of admissible ordinals, it is tempting to focus one's attention on some specific ordinals whose characteristics admit a more detailed analysis of the fine structure of sets and degrees. From this point of view,
) is a natural class to study can be seen from the role played by its ω-counterpart in the study of decision problems and automorphisms of ℰ*(ω), the lattice of ω-r.e. sets modulo finite sets (Soare [13] gives an extensive literature on these topics). In α-recursion theory the existence of hh-simple sets is not an all pervasive phenomenon, and there is as yet no complete characterization of the admissible ordinal α for which ℋ(α) is nonempty. While this situation is admittedly unsatisfactory, we feel that the lattice ℰ*(α) of α-r.e. sets modulo α*-finite sets for which ℋ(α) ≠ ∅ deserves a careful study. Indeed armed with some understanding over the last few years of the general theory of admissible ordinals, it is tempting to focus one's attention on some specific ordinals whose characteristics admit a more detailed analysis of the fine structure of sets and degrees. From this point of view, 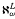 and ℋ(
and ℋ(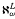 ) are natural objects of study since the former is a typical example of a non-Σ2-projectible, Σ2-inadmissible ordinal, while the latter is important for the investigations of automorphisms over ℰ*(
) are natural objects of study since the former is a typical example of a non-Σ2-projectible, Σ2-inadmissible ordinal, while the latter is important for the investigations of automorphisms over ℰ*(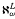 ).
).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983


