Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T17:07:46.141Z Has data issue: false hasContentIssue false
  • English
  • Français

HTP-COMPLETE RINGS OF RATIONAL NUMBERS

Part of: Computability and recursion theory Connections with logic Model theory

Published online by Cambridge University Press:  22 November 2021

RUSSELL MILLER Open the ORCID record for RUSSELL MILLER [Opens in a new window]
RUSSELL MILLER*
Affiliation:
DEPARTMENT OF MATHEMATICS QUEENS COLLEGE, THE CITY UNIVERSITY OF NEW YORK 65-30 KISSENA BOULEVARD QUEENS, NY11367, USA PHD PROGRAMS IN MATHEMATICS AND COMPUTER SCIENCE CUNY GRADUATE CENTER 365 FIFTH AVENUE NEW YORK, NY10016, USAE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a ring R, Hilbert’s Tenth Problem 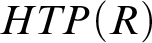$HTP(R)$ is the set of polynomial equations over R, in several variables, with solutions in R. We view 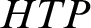$HTP$ as an enumeration operator, mapping each set W of prime numbers to 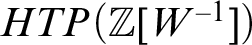$HTP(\mathbb {Z}[W^{-1}])$ , which is naturally viewed as a set of polynomials in 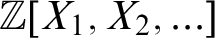$\mathbb {Z}[X_1,X_2,\ldots ]$ . It is known that for almost all W, the jump 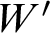$W'$ does not 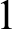$1$ -reduce to 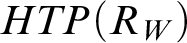$HTP(R_W)$ . In contrast, we show that every Turing degree contains a set W for which such a 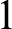$1$ -reduction does hold: these W are said to be HTP-complete. Continuing, we derive additional results regarding the impossibility that a decision procedure for 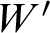$W'$ from 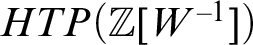$HTP(\mathbb {Z}[W^{-1}])$ can succeed uniformly on a set of measure 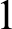$1$ , and regarding the consequences for the boundary sets of the 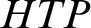$HTP$ operator in case 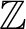$\mathbb {Z}$ has an existential definition in 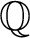$\mathbb {Q}$ .

Keywords

boundary setscomputability theoryHilbert’s Tenth ProblemHTP-completenesssubrings of the rational numbers

MSC classification

Primary: 12L05: Decidability 03D45: Theory of numerations, effectively presented structures 03C40: Interpolation, preservation, definability
Type
Article
Information
The Journal of Symbolic Logic , Volume 87 , Issue 1 , March 2022 , pp. 252 - 272
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Davis, M., Putnam, H., and Robinson, J., The decision problem for exponential Diophantine equations . Annals of Mathematics. Second Series, vol. 74 (1961), no. 3, pp. 425–436.CrossRefGoogle Scholar
Eisenträger, K., Miller, R., Park, J., and Shlapentokh, A., As easy as ℚ: Hilbert’s tenth problem for subrings of the rationals . Transactions of the American Mathematical Society, vol. 369 (2017), no. 11, pp. 8291–8315.10.1090/tran/7075CrossRefGoogle Scholar
Friedberg, R. M., A criterion for completeness of degrees of unsolvability, this Journal, vol. 22 (1957), pp. 159–160.Google Scholar
Jockusch, C. G. Jr., Degrees of generic sets , Recursion Theory: Its Generalisation and Applications (Proceedings of Logic Colloquium, University of Leeds, Leeds, 1979) (F. R. Drake and S. S. Wainer, editors), London Mathematical Society Lecture Note Series, vol. 45, Cambridge University Press, Cambridge, 1981, pp. 110–139.CrossRefGoogle Scholar
Jockusch, C. G. Jr. and Shore, R. A., Pseudo jump operators I: The r.e. case . Transactions of the American Mathematical Society, vol. 275 (1983), no. 2, pp. 599–609.Google Scholar
Jockusch, C. G. Jr. and Shore, R. A., Pseudo-jump operators II: Transfinite iterations, hierarchies, and minimal covers, this Journal, vol. 49 (1984), pp. 1205–1236.Google Scholar
Koenigsmann, J., Defining ℤ in ℚ . Annals of Mathematics. Second Series, vol. 183 (2016), no. 1, pp. 73–93.CrossRefGoogle Scholar
Kramer, K. and Miller, R., The Hilbert’s-tenth-problem operator . Israel Journal of Mathematics, vol. 230 (2019), no. 2, pp. 693–713.10.1007/s11856-019-1833-2CrossRefGoogle Scholar
Kurtz, S., Randomness and genericity in the degrees of unsolvability , Ph.D. thesis, University of Illinois at Urbana-Champaign, 1981.Google Scholar
Matiyasevich, Y. V., The Diophantineness of enumerable sets . Doklady Akademii Nauk SSSR, vol. 191 (1970), pp. 279–282.Google Scholar
Miller, R., Computable fields and Galois theory . Notices of the American Mathematical Society, vol. 55 (2008), no. 7, pp. 798–807.Google Scholar
Miller, R., Baire category theory and Hilbert’s tenth problem inside ℚ , Pursuit of the Universal: 12th Conference on Computability in Europe, CiE 2016 (A. Beckmann, L. Bienvenu, and N. Jonoska, editors), Lecture Notes in Computer Science, vol. 9709, Springer, Cham, 2016, pp. 343–352.CrossRefGoogle Scholar
Miller, R., Measure theory and Hilbert’s tenth problem inside ℚ , Sets and Computations (S. D. Friedman, D. Raghavan, and Y. Yang, editors), Lecture Note Series, vol. 33, World Scientific Publishing Co., Singapore, 2017, pp. 253–269.10.1142/9789813223523_0010CrossRefGoogle Scholar
Poonen, B., Hilbert’s tenth problem and Mazur’s conjecture for large subrings of ℚ . Journal of the American Mathematical Society, vol. 16 (2003), no. 4, pp. 981–990.CrossRefGoogle Scholar
Poonen, B., Characterizing integers among rational numbers with a universal-existential formula . American Journal of Mathematics, vol. 131 (2009), no. 3, pp. 675–682.10.1353/ajm.0.0057CrossRefGoogle Scholar
Robinson, J., Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114.Google Scholar
Rogers, H., Theory of Recursive Functions and Effective Computability, McGraw-Hill, New York, 1967.Google Scholar
Serre, J.-P., A Course in Arithmetic, Graduate Texts in Mathematics, vol. 7, Springer, Berlin, 1973.10.1007/978-1-4684-9884-4CrossRefGoogle Scholar
Shlapentokh, A., Hilbert’s Tenth Problem: Diophantine Classes and Extensions to Global Fields, Cambridge University Press, Cambridge, 2007.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, Springer, Berlin, 1987.CrossRefGoogle Scholar