Article contents
Horn sentences in identity theory1
Published online by Cambridge University Press: 12 March 2014
Extract
Horn [2] obtained a sufficient condition for an elementary class to be closed under direct product. Chang and Morel [1] showed that this is not a necessary condition. We will show that, if consideration is restricted to identity theory, that is, a first-order predicate calculus with equality but no other relation symbols or operation symbols, Horn's condition is necessary and sufficient.
A model 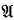 for identity theory consists of a non-empty domain A, but no relations or operations except equality. If I is an index set, and for each
for identity theory consists of a non-empty domain A, but no relations or operations except equality. If I is an index set, and for each  is a model for identity theory, then the direct product
is a model for identity theory, then the direct product 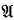 of the
of the  is a model for identity theory and has domain A, the cartesian product of the Ai.
is a model for identity theory and has domain A, the cartesian product of the Ai.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1952
Footnotes
This paper is a portion of a dissertation submitted to the graduate school of the University of Michigan in partial fulfillment of the requirements for the Ph.D. degree. The author wishes to thank Professor R. C. Lyndon for his guidance and encouragement and Professor John Addison for his many suggestions.
References
- 7
- Cited by


