Published online by Cambridge University Press: 12 March 2014
Let ε stand for the set of nonnegative integers (numbers), V for the class of all subcollections of ε (sets), Λ for the set of isols, and 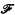 for the set of mappings from a subset of ε into ε (functions). I f is a function we write δf and ρf for its domain and range respectively. The relation of inclusion is denoted by ⊂ and that of proper inclusion by ⊊. The sets α and β are recursively equivalent [written: α ≃ β], if δf = α and ρf = β for some function f with a one-to-one partial recursive extension f. We denote the recursive equivalence type of α, {σ ∈ V ∣ ≃ α}, by Req(α). Also R stands for Req(ε), while ΛR denotes the collection of all regressive isols. The reader is assumed to be familiar with the contents of [1] and [6].
for the set of mappings from a subset of ε into ε (functions). I f is a function we write δf and ρf for its domain and range respectively. The relation of inclusion is denoted by ⊂ and that of proper inclusion by ⊊. The sets α and β are recursively equivalent [written: α ≃ β], if δf = α and ρf = β for some function f with a one-to-one partial recursive extension f. We denote the recursive equivalence type of α, {σ ∈ V ∣ ≃ α}, by Req(α). Also R stands for Req(ε), while ΛR denotes the collection of all regressive isols. The reader is assumed to be familiar with the contents of [1] and [6].
The results presented in this paper were taken from the author's doctoral dissertation written at Rutgers University under the direction of Professor J. C. E. Dekker.