Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T10:06:44.264Z Has data issue: false hasContentIssue false
  • English
  • Français

Hechler's Theorem for tall analytic P-ideals

Published online by Cambridge University Press:  12 March 2014

Barnabás Farkas
Barnabás Farkas*
Affiliation:
Institute of Mathematics, Budapest University of Technology and Economics, Egry Jozsef U. 1 (Building H), 1111 Budapest, Hungary, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the following version of Hechler's classical theorem: For each partially ordered set (Q, ≤) with the property that every countable subset of Q has a strict upper bound in Q, there is a ccc forcing notion such that in the generic extension for each tall analytic P-ideal 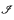(coded in the ground model) a cofinal subset of 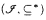is order isomorphic to (Q, ≤).

Keywords

Hechler's Theoremforcinganalytic P-ideals
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 729 - 736
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartoszynski, Tomek and Kada, Masaru, Hechler's theorem for the meager ideal, Topology and its Applications, vol. 146–147 (2005), pp. 429–435.CrossRefGoogle Scholar
[2]Burke, Maxim R., A proof of Heckler's theorem on embedding ℵ1-directed sets cofinally into (ωω, <*), Archive for Mathematical Logic, vol. 36 (1997), pp. 399–403.CrossRefGoogle Scholar
[3]Burke, Maxim R. and Kada, Masaru, Hechler's theorem for the null ideal, Archive for Mathematical Logic, vol. 43 (2004), pp. 703–722.CrossRefGoogle Scholar
[4]Fremlin, David H., Measure theory. Set-theoretic measure theory, Torres Fremlin, Colchester, England, 2004, available at http://www.essex.ac.uk/maths/staff/fremlin/mt.html.Google Scholar
[5]Hechler, S. H., On the existence of certain cofinal subsets of ωω, Axiomatic set theory (Jech, Thomas, editor), American Mathematical Society, 1974, pp. 155–173.CrossRefGoogle Scholar
[6]Solecki, Slamowir, Analytic P-ideals and their applications, Annals of Pure and Applied Logic, vol. 99 (1999), pp. 51–72.CrossRefGoogle Scholar
[7]Soukup, Lajos, Pcf theory and cardinal invariants of the reals, unpublished notes, 2001.Google Scholar