Article contents
Grzegorcyk's hierarchy and IepΣ1
Published online by Cambridge University Press: 12 March 2014
Extract
A proof-theoretic characterization of the primitive recursive functions is the Σ1-definable functions in IΣ1 as is shown in Mints [4], Parsons [5], and [8].
Then what is a proof-theoretic characterization of Grzegorzyk's hierarchy? First we discuss a related previous work. In Clote and Takeuti [2], we introduced a theory TAC that corresponds to the computational complexity class AC. TAC has a very weak form of induction. We assign a rank to a proof in TAC in the following way. The rank of a proof P in TAC is the nesting number of inductions used in P. Then TACi is defined to be the subtheory of TAC whose proof has a rank ≤ i. We proved that TACi corresponds to the class ACi.
In this paper we introduce a theory IepΣ1 which is equivalent to IΣ1. Then we define the rank of a proof in IepΣ1 as the nesting number of inductions in the proof and prove that the proofs with rank ≤ i correspond to Grzegorcyk's hierarchy 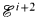 for i > 0.
for i > 0.
We also prove that the system that has proofs with rank 0 is actually equivalent to I Δ0. These facts are interesting since it is proved in [10] that the theory isomorphic to TAC∘ by RSUV isomorphism is a conservative extension of I Δo. Therefore there is some analogy between the class AC and the primitive recursive functions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1994
References
REFERENCES
- 4
- Cited by


