Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T20:30:56.384Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GENERIC DEGREES OF DENSITY-1 SETS, AND A CHARACTERIZATION OF THE HYPERARITHMETIC REALS

Published online by Cambridge University Press:  22 December 2015

GREGORY IGUSA
GREGORY IGUSA*
Affiliation:
UNIVERSITY OF NOTRE DAME DEPARTMENT OF MATHEMATICS 255 HURLEY, NOTRE DAME, IN 46556, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A generic computation of a subset A of ℕ is a computation which correctly computes most of the bits of A, but which potentially does not halt on all inputs. The motivation for this concept is derived from complexity theory, where it has been noticed that frequently, it is more important to know how difficult a type of problem is in the general case than how difficult it is in the worst case. When we study this concept from a recursion theoretic point of view, to create a transitive relationship, we are forced to consider oracles that sometimes fail to give answers when asked questions. Unfortunately, this makes working in the generic degrees quite difficult. Indeed, we show that generic reduction is 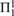$\Pi _1^1$―complete. To help avoid this difficulty, we work with the generic degrees of density-1 reals. We demonstrate how an understanding of these degrees leads to a greater understanding of the overall structure of the generic degrees, and we also use these density-1 sets to provide a new a characterization of the hyperartithmetical Turing degrees.

Keywords

recursion theorycomputabilitygeneric computabilitydegree structures
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1290 - 1314
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Gurevich, Yuri, Average case completeness. Journal of Computer and System Sciences, vol. 42 (1991), no. 3, pp. 346–398. Twenty-Eighth IEEE Symposium on Foundations of Computer Science (Los Angeles, CA, 1987).CrossRefGoogle Scholar
Igusa, Gregory, Nonexistence of minimal pairs for generic computability, this Journal, 78 (2): 511–522 (2013).CrossRefGoogle Scholar
Jockusch, Carl G. Jr. and Schupp, Paul E., Generic computability, Turing degrees, and asymptotic density. Journal of the London Mathematical Society (2), vol. 85 (2012), no. 2, pp. 472–490.CrossRefGoogle Scholar
Kapovich, Ilya, Miasnikov, Alexei, Schupp, Paul, and Shpilrain, Vladimir, Generic-case complexity, decision problems in group theory, and random walks. Journal of Algebra, vol. 264 (2003), no. 2, pp. 665–694.CrossRefGoogle Scholar
Sacks, Gerald E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Soare, Robert I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic, A study of computable functions and computably generated sets, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar
Solovay, Robert M., Hyperarithmetically encodable sets. Transactions of the American Mathematical Society, vol. 239 (1978), pp. 99–122.CrossRefGoogle Scholar