Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T01:54:29.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Forcing isomorphism II

Published online by Cambridge University Press:  12 March 2014

M. C. Laskowski  and
S. Shelah
M. C. Laskowski
Affiliation:
Department of Mathematics, University of Maryland, College Park, Maryland 20742, USA, E-mail: [email protected]
S. Shelah
Affiliation:
School of Mathematics, The Hebrew University, Jerusalem, Israel Department of Mathematics, Rutgers University, New Brunswick, NJ 08903, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If T has only countably many complete types, yet has a type of infinite multiplicity then there is a c.c.c. forcing notion 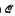such that, in any 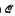-generic extension of the universe, there are non-isomorphic models M1 and M2 of T that can be forced isomorphic by a c.c.c. forcing. We give examples showing that the hypothesis on the number of complete types is necessary and what happens if ‘c.c.c’ is replaced by other cardinal-preserving adjectives. We also give an example showing that membership in a pseudo-elementary class can be altered by very simple cardinal-preserving forcings.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 4 , December 1996 , pp. 1305 - 1320
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T., Fundamentals of stability theory, Springer-Verlag, 1988.CrossRefGoogle Scholar
[2]Baldwin, J. T., Laskowski, M. C., and Shelah, S., Forcing isomorphism, this Journal, vol. 58 (1993).Google Scholar
[3]Barwise, J., Back and forth through infinitary logic, Studies in model theory (Morley, M., editor), Mathematical Association of America, 1973, pp. 5–34.Google Scholar
[4]Kunen, K., Set theory, North-Holland, 1980.Google Scholar
[5]Lascar, D., Stability in model theory, Longman, 1987, originally published in French as Stabilité en Théorie des Modèles, 1986.Google Scholar
[6]Makkai, M., Survey of basic stability with particular emphasis on orthogonality and regular types, Israel Journal of Mathematics (1984).CrossRefGoogle Scholar
[7]Nachbin, L., The Haar integral, van Nostrand, 1965.Google Scholar
[8]Shelah, S., Existence of many L∞,λ-equivalent non-isomorphic models of T of power λ, Annals of Pure and Applied Logic, vol. 34 (1987).CrossRefGoogle Scholar
[9]Shelah, S., Classification theory, North-Holland, 1991.Google Scholar