Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T19:43:10.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Forcing and reducibilities. III. Forcing in fragments of set theory

Published online by Cambridge University Press:  12 March 2014

Piergiorgio Odifreddi
Piergiorgio Odifreddi*
Affiliation:
University of Turin, Turin, Italy
Get access Rights & Permissions [Opens in a new window]

Extract

We conclude here the treatment of forcing in recursion theory begun in Part I and continued in Part II of [31]. The numbering of sections is the continuation of the numbering of the first two parts. The bibliography is independent.

In Part I our language was a first-order language: the only set we considered was the (set constant for the) generic set. In Part II a second-order language was introduced, and we had to interpret the second-order variables in some way. What we did was to consider the ramified analytic hierarchy, defined by induction as:

A0 = {X ⊆ ω: X is arithmetic},

Aα+1 = {X ⊆ ω: X is definable (in 2nd order arithmetic) over Aα},

Aλ = ⋃α<λAα (λ limit),

RA = ⋃αAα.

We then used (a relativized version of) the fact that 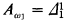(Kleene [27]). The definition of RA is obviously modeled on the definition of the constructible hierarchy introduced by Gödel [14]. For this we no longer work in a language for second-order arithmetic, but in a language for (first-order) set theory with membership as the only nonlogical relation:

L0 = ⊘,

Lα+1 = {X: X is (first-order) definable over Lα},

Lλ = ⋃α<λLα (λ limit),

L = ⋃αLα.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 1013 - 1034
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Abramson, F.G., Sacks forcing does not always produce a minimal upper bound, Advances in Mathematics, vol. 31 (1979), pp. 110–130.CrossRefGoogle Scholar
[2]Adamowicz, Z., On finite lattices of degrees of constructibilily of reals, this Journal, vol. 41 (1976), pp. 313–322.Google Scholar
[3]Adamowicz, Z., Constructible semi-lattices of degrees of constructibility, Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin and New York, 1977, pp. 1–44.Google Scholar
[4]Addison, J. W., Some consequences of the axiom of constructibility, Fundamenta Mathematicae, vol. 46 (1959), pp. 337–357.CrossRefGoogle Scholar
[5]Addison, J.W. and Kleene, S.C., A note on function quantification, Proceedings of the American Mathematical Society, vol. 8 (1957), pp. 1002–1006.CrossRefGoogle Scholar
[6]Balcar, B. and Hajek, P., On sequences of degrees of constructibility, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 24 (1978), pp. 291–296.CrossRefGoogle Scholar
[7]Barwise, J., Admissible sets and structure, Springer-Verlag, Berlin and New York, 1975.CrossRefGoogle Scholar
[8]Boolos, G. and Putnam, H., Degrees of unsolvability of constructible sets of integers, this Journal, vol. 33 (1968), pp. 497–513.Google Scholar
[9]Devlin, K.J., Aspects of constructibility, Lecture Notes in Mathematics, vol. 354, Springer-Verlag, Berlin and New York, 1973.Google Scholar
[10]Epstein, R.L., Degrees of unsolvability: Structure and theory, Lecture Notes in Mathematics, vol. 759, Springer-Verlag, Berlin and New York, 1979.Google Scholar
[11]Feferman, S., Some applications of the notion of forcing and generic sets, Fundamenta Mathematicae, vol. 56 (1965), pp. 325–345.CrossRefGoogle Scholar
[12]Friedman, H., Minimality in the -degrees, Fundamenta Mathematicae, vol. 81 (1974), pp. 183–192.CrossRefGoogle Scholar
[13]Friedman, H. and Jensen, R., Note on admissible ordinals, Lecture Notes in Mathematics, vol. 72, Springer-Verlag, Berlin and New York, 1968, pp. 77–79.Google Scholar
[14]Gödel, K., The consistency of the axiom of choice and the generalized continuum hypothesis, Proceedings of the National Academy of Sciences of the U.S.A., vol. 24 (1938), pp. 556–557.CrossRefGoogle ScholarPubMed
[15]Guaspari, D., Characterizing the constructive reals, L'Académie Polonaise des Sciences Bulletin Série des Sciences Mathématiques, vol. 22 (1974), pp. 357–358.Google Scholar
[16]Grilliott, T.J., Omitting types: applications to recursion theory, this Journal, vol. 37 (1972), pp. 81–89.Google Scholar
[17]Hajek, P., Some results on degrees of constructibility, Lecture Notes in Mathematics, vol. 669, Springer-Verlag, Berlin and New York, 1978, pp. 55–71.Google Scholar
[18]Harrington, L., Analytic determinacy and 0#, this Journal, vol. 43 (1978), pp. 685–693.Google Scholar
[19]Harrington, L. and Kechris, A., singletons and 0#, Fundamenta Mathematicae, vol. 95 (1977), pp. 167–171.CrossRefGoogle Scholar
[20]Harrison, J., Some applications of recursive pseudo-well orderings, Doctoral dissertation, Stanford University, Stanford, California, 1967.Google Scholar
[21]Jensen, R., Definable sets of minimal degree, Mathematical logic and foundations of set theory (Bar-Hillel, H., Editor), North-Holland, Amsterdam 1970, pp. 122–128.Google Scholar
[22]Jensen, R. and Solovay, R. M., Some applications of almost disjoint sets, Mathematical logic and foundations of set theory (Bar-Hillel, H., Editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
[23]Kechris, A., The theory of countable analytical sets, Transactions of the American Mathematical Society, vol. 202 (1975), pp. 259–297.CrossRefGoogle Scholar
[24]Kechris, A., Minimal upper bounds for sequences of -degrees, this Journal, vol. 43 (1978), pp. 502–507.Google Scholar
[25]Kechris, A., Forcing in analysis, Lecture Notes in Mathematics, vol. 669, Springer-Verlag, Berlin and New York, 1978, pp. 278–302.Google Scholar
[26]Kechris, A., Forcing with ⊿ perfect trees and minimal ⊿-degrees, this Journal, vol. 46 (1981), pp. 803–816.Google Scholar
[27]Kleene, S.C., Quantification over number-theoretic functions, Compositio Mathematicae, vol. 14(1959), pp. 23–40.Google Scholar
[28]Moschovakis, Y., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[29]Nerode, A. and Shore, R. A., Second order logic and first order theories of reducibility orderings, Proceedings of the Kleene Symposium, North-Holland, Amsterdam, 1980.Google Scholar
[30]Maass, W., Recursively enumerable generic sets, this Journal, vol. 47 (1982), pp. 809–823.Google Scholar
[31]Odifreddi, P.G., Forcing and reducibilities, I, II, this Journal, vol. 48 (1983), pp. 288–310, 724–743.Google Scholar
[32]Odifreddi, P.G., Classical recursion theory (to appear).Google Scholar
[33]Richter, W., Constructive transfinite number classes, Bulletin of the American Mathematical Society, vol. 73 (1967), pp. 261–265.CrossRefGoogle Scholar
[34]Sacks, G.E., Forcing with perfect closed sets, Proceedings of Symposia in Pure Mathematics, vol. 13, Part I, American Mathematical Society, Providence, RI., 1971, pp. 331–355.Google Scholar
[35]Sacks, G.E., On the reducibility of sets, Advances in Mathematics, vol. 7 (1971), pp. 57–72.CrossRefGoogle Scholar
[36]Sacks, G.E., The 1-sections of a type n obiect, Generalized recursion theory (Fenstad, J. and Hinman, P., Editors), North-Holland, Amsterdam, 1974, pp. 81–93.Google Scholar
[37]Sacks, G.E., Countable admissible ordinals and hyperdegrees, Advances in Mathematics, vol. 19(1976), pp. 213–262.CrossRefGoogle Scholar
[38]Shoenfield, J.R., The problem of predicativity, Essays on the foundations of mathematics, Magnes Press, Jerusalem, 1961, pp. 132–139.Google Scholar
[39]Shoenfield, J.R., The form of the negation of a predicate, Proceedings of Symposia in Pure Mathematics, vol. 6 American Mathematical Society, Providence, R.I., 1962, pp. 131–134.Google Scholar
[40]Shoenfield, J.R., Mathematical logic, Addison-Wesley, Reading, Mass., 1967.Google Scholar
[41]Silver, J., Some applications of model theory in set theory, Annals of Mathematical Logic, vol. 3(1971), pp. 45–110.CrossRefGoogle Scholar
[42]Simpson, S G., Minimal covers and hyperdegrees, Transactions of the American Mathematical Society, vol. 209 (1975), pp. 45–64.CrossRefGoogle Scholar
[43]Solovay, R.M., A non-constructible set of integers, Transactions of the American Mathematical Society, vol. 127 (1967), pp. 58–75.Google Scholar
[44]Solovay, R.M., On the cardinality of sets of reals, Foundations of mathematics (Bulloff, J.et al., eds) Springer-Verlag, Berlin and New York, 1969, pp. 58–73.CrossRefGoogle Scholar
[45]Spector, C., Recursive ordinals and predicative set theory, mimeographed notes, Summer Institute for Symbolic Logic, Cornell University, Ithaca, New York, 1957.Google Scholar
[46]Steen, J. R., Forcing with tagged trees, Annals of Mathematical Logic, vol. 15 (1978), pp. 55–74.Google Scholar
[47]Suzuki, Y., A complete classification of the functions, Bulletin of the American Mathematical Society, vol. 70 (1964), pp. 246–253.CrossRefGoogle Scholar
[48]Tarski, A., Logic, semantics, metamathematics, Oxford University Press, Oxford, 1956.Google Scholar
[49]Tugue, T., Predicates recursive in a type-2 object and Kleene hierarchies, Commentarii Mathematici Universitatis Sancti Pauli, vol. 8 (1960), pp. 97–117.Google Scholar
[50]Zarach, A., Generic extensions of admissible sets, Lecture Notes in Mathematics, vol. 537, Springer-Verlag, Berlin and New York, 1976, pp. 321–333.Google Scholar