Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Melleray, Julien
and
Tsankov, Todor
2013.
Generic representations of abelian groups and extreme amenability.
Israel Journal of Mathematics,
Vol. 198,
Issue. 1,
p.
129.
Glasner, Y.
Kitroser, D.
and
Melleray, J.
2016.
From isolated subgroups to generic permutation representations.
Journal of the London Mathematical Society,
Vol. 94,
Issue. 3,
p.
688.
Doucha, Michal
and
Malicki, Maciej
2019.
Generic representations of countable groups.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 11,
p.
8249.
Doucha, Michal
2019.
Universal actions and representations of locally finite groups on metric spaces.
Israel Journal of Mathematics,
Vol. 231,
Issue. 1,
p.
343.
Etedadialiabadi, Mahmood
Gao, Su
Le Maître, François
and
Melleray, Julien
2021.
Dense locally finite subgroups of automorphism groups of ultraextensive spaces.
Advances in Mathematics,
Vol. 391,
Issue. ,
p.
107966.
Hubička, Jan
Konečný, Matěj
and
Nešetřil, Jaroslav
2022.
All those EPPA classes (strengthenings of the Herwig–Lascar theorem).
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 11,
p.
7601.
GAO, SU
and
REN, XUANZHI
2024.
THE AMALGAMATION PROPERTY AND URYSOHN STRUCTURES IN CONTINUOUS LOGIC.
The Journal of Symbolic Logic,
p.
1.
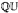 ) of all actions of Γ by isometries of the rational Urysohn metric space
) of all actions of Γ by isometries of the rational Urysohn metric space 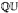 , where Isom (Γ,
, where Isom (Γ, 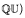 ) is equipped with the topology it inherits seen as a closed subset of Isom
) is equipped with the topology it inherits seen as a closed subset of Isom 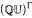 . When Γ is the free group
. When Γ is the free group 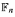 on n generators this space is just Isom
on n generators this space is just Isom 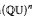 , but is in general significantly more complicated. We prove that when Γ is finitely generated Abelian there is a generic point in Isom(Γ,
, but is in general significantly more complicated. We prove that when Γ is finitely generated Abelian there is a generic point in Isom(Γ, 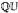 ), i.e., there is a comeagre set of mutually conjugate isometric actions of Γ on
), i.e., there is a comeagre set of mutually conjugate isometric actions of Γ on 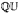 .
.