Article contents
Fields interpretable in superrosy groups with NIP (the non-solvable case)
Published online by Cambridge University Press: 12 March 2014
Abstract
Let G be a group definable in a monster model 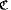 of a rosy theory satisfying NIP. Assume that G has hereditarily finitely satisfiable generics and 1 < U b(G) < ∞. We prove that if G acts definably on a definable set of U р-rank 1, then, under some general assumption about this action, there is an infinite field interpretable in
of a rosy theory satisfying NIP. Assume that G has hereditarily finitely satisfiable generics and 1 < U b(G) < ∞. We prove that if G acts definably on a definable set of U р-rank 1, then, under some general assumption about this action, there is an infinite field interpretable in 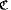 . We conclude that if G is not solvable-by-finite and it acts faithfully and definably on a definable set of U р-rank 1, then there is an infinite field interpretable in
. We conclude that if G is not solvable-by-finite and it acts faithfully and definably on a definable set of U р-rank 1, then there is an infinite field interpretable in 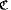 . As an immediate consequence, we get that if G has a definable subgroup H such that U р(G) = U р(H) + 1 and G/⋂g∈G Hg is not solvable-by-finite, then an infinite field interpretable in
. As an immediate consequence, we get that if G has a definable subgroup H such that U р(G) = U р(H) + 1 and G/⋂g∈G Hg is not solvable-by-finite, then an infinite field interpretable in 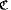 also exists.
also exists.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2010
References
REFERENCES
- 2
- Cited by


