No CrossRef data available.
Published online by Cambridge University Press: 21 March 2017
In this paper, we prove the decidability of the theory of ℚp in the language (+, −,⋅, 0, 1, Pn(n ∈ ℕ)) expanded by a predicate for the multiplicative subgroup nℤ (where n is a fixed integer). There are two cases: if 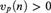 $v_p \left( n \right) > 0$ then the group determines a cross-section and we get an axiomatization of the theory and a result of quantifier elimination. If
$v_p \left( n \right) > 0$ then the group determines a cross-section and we get an axiomatization of the theory and a result of quantifier elimination. If 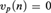 $v_p \left( n \right) = 0$, then we use the Mann property of the group to get an axiomatization of the theory.
$v_p \left( n \right) = 0$, then we use the Mann property of the group to get an axiomatization of the theory.