Article contents
Explicit mathematics with the monotone fixed point principle
Published online by Cambridge University Press: 12 March 2014
Abstract
The context for this paper is Feferman's theory of explicit mathematics, a formal framework serving many purposes. It is suitable for representing Bishop-style constructive mathematics as well as generalized recursion, including direct expression of structural concepts which admit self-application. The object of investigation here is the theory of explicit mathematics augmented by the monotone fixed point principle, which asserts that any monotone operation on classifications (Feferman's notion of set) possesses a least fixed point. To be more precise, the new axiom not merely postulates the existence of a least solution, but, by adjoining a new functional constant to the language, it is ensured that a fixed point is uniformly presentable as a function of the monotone operation.
The upshot of the paper is that the latter extension of explicit mathematics (when based on classical logic) embodies considerable proof-theoretic strength. It is shown that it has at least the strength of the subsystem of second order arithmetic based on 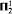 comprehension.
comprehension.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 5
- Cited by


